摘要:已知.梯形ABCD中.BC∥AD.∠C=90°.BD⊥AB.AD=25.BC=16.将∠CDB绕点D顺时针旋转.旋转后角的两边分别交直线AB于C´.B´.射线DC´交射线CB于P. (1)点P.B´分别在线段CB.BA上时..判断△PDB´的形状并加以证明, (2)点P.B´分别在射线CB.BA上.且tan∠PB´C´=时.求线段B´C´的长, (3)当∠CDB旋转至被BD平分时.求点P到DB´的距离.
网址:http://m.1010jiajiao.com/timu3_id_471009[举报]
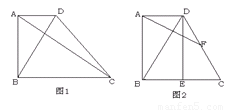
已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
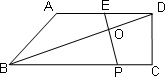
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为k,若AD∶BC=2∶3.请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当k=1时,是________;②当k=2时,是________;③当k=3时,是________.并证明k=2时的结论.
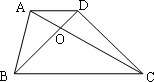
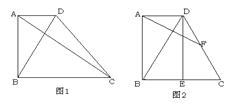
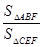 = .
= .
 = .
= .