摘要:22.已知如图.在△ABC中.∠C=900.点M在BC上.且BM=AC.点N在AC上.且AN=MC.AM和BN相交于P.求∠BPM的度数.
网址:http://m.1010jiajiao.com/timu3_id_469315[举报]
如图:已知△ABC中,AB=AC,∠BAC=900,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于E、F,给出以下五个结论: ①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④![]() S△ABC;⑤EF=AP。当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有 ( )
S△ABC;⑤EF=AP。当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有 ( )
A.2个 B.3个 C.4个 D.5个

(7分)阅读材料,解答问题:
命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,ΔABC的外接圆半径为R,
则![]() 2R.
2R.
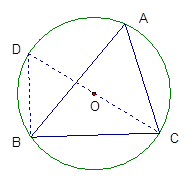
证明:连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,因为CD是⊙O的直径,所以∠DBC=900,在Rt△DBC中,sinD=![]() ,所以sinA=
,所以sinA=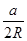 ,即
,即![]() ,同理:
,同理:![]() , ∴
, ∴ ![]() 2R.
2R.
请阅读前面所给的命题和证明后,完成下面(1)(2)两题:
1.(1)前面阅读材料中省略了“![]() ”的证明过程,请你把“
”的证明过程,请你把“![]() ”的证明过程补写出来.
”的证明过程补写出来.
2.(2)直接运用阅读材料中命题的结论解题:已知锐角△ABC中, BC=![]() ,CA=
,CA=![]() ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.
查看习题详情和答案>>
(7分)阅读材料,解答问题:
命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,ΔABC的外接圆半径为R,
则 2R.
2R.

证明:连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,因为CD是⊙O的直径,所以∠DBC=900,在Rt△DBC中,sinD= ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  2R.
2R.
请阅读前面所给的命题和证明后,完成下面(1)(2)两题:
【小题1】(1)前面阅读材料中省略了“ ”的证明过程,请你把“
”的证明过程,请你把“ ”的证明过程补写出来.
”的证明过程补写出来.
【小题2】(2)直接运用阅读材料中命题的结论解题:已知锐角△ABC中, BC= ,CA=
,CA=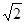 ,∠A=600,求△ABC的外接圆半径 R及∠C.
查看习题详情和答案>>
,∠A=600,求△ABC的外接圆半径 R及∠C.
查看习题详情和答案>>
命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,ΔABC的外接圆半径为R,
则
 2R.
2R. 
证明:连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,因为CD是⊙O的直径,所以∠DBC=900,在Rt△DBC中,sinD=
 ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  2R.
2R.请阅读前面所给的命题和证明后,完成下面(1)(2)两题:
【小题1】(1)前面阅读材料中省略了“
 ”的证明过程,请你把“
”的证明过程,请你把“ ”的证明过程补写出来.
”的证明过程补写出来. 【小题2】(2)直接运用阅读材料中命题的结论解题:已知锐角△ABC中, BC=
 ,CA=
,CA=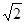 ,∠A=600,求△ABC的外接圆半径 R及∠C.
查看习题详情和答案>>
,∠A=600,求△ABC的外接圆半径 R及∠C.
查看习题详情和答案>>
 2R.
2R. 
 ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  ”的证明过程补写出来.
”的证明过程补写出来.  ,CA=
,CA= ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C. 2R.
2R. 
 ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  ”的证明过程补写出来.
”的证明过程补写出来.  ,CA=
,CA= ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.