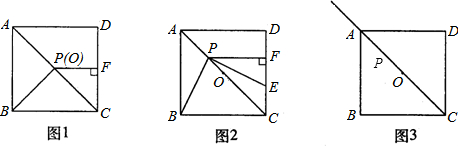
⑴ ①略,②PC-PA＝CE,⑵结论①仍成立,结论②不成立.此时②中三条线段的数量关系是PA-PC＝CE,——青夏教育精英家教网——

摘要： ⑴ ①略,②PC-PA＝CE,⑵结论①仍成立,结论②不成立.此时②中三条线段的数量关系是PA-PC＝CE,

网址：http://m.1010jiajiao.com/timu3_id_467746[举报]

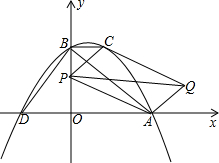如图，已知二次函数y=ax²+bx+c的图象与x轴交于点A（5，0），与y轴交于点B，过点B作BC⊥y轴，BC与函数y=ax²+bx+c的图象交于点C（2，4）．
（1）设函数y=ax²+bx+c的图象与x轴的另一个交点为D，求△BDA的面积．
（2）若P为y轴上的一个动点，连接PA、PC，分别过A、C作PC、PA的平行线交于点Q，连接PQ．试探究：
①是否存在点P，使得PQ²=PA²+PC²？请说明理由．
②是否存在点P，使得PQ取得最小值？若存在，请求出这个最小值，并求出此时点P的坐标；若不存在，请说明理由．

查看习题详情和答案>>

阅读理解与应用
如图，⊙O₁与⊙O₂交于A，B两点，C，D是⊙O₁上的两点，E，F是⊙O₂上的两点，BA的延长线、DC的延长线、FE的延长线都交于点P．
通过证明△PBC与△PDA相似，得到的比例式化成等积式为：PC•PD=PA•PB．
问题：（1）PE•PF=PA•PB成立吗？为什么？
（2）直接写出PC•PD与PE•PF的数量关系式．

查看习题详情和答案>>

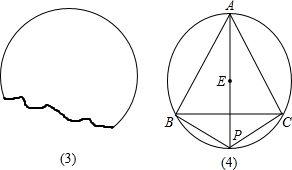
（1）试找出如图3所示的破残轮片的圆心的位置；（不写作法，保留作图痕迹）
（2）如图4，在等边△ABC外接圆劣弧

上任取一点P，连接PA、PB、PC，判断结论“PB+PC＞PA”是否正确，若正确请证明，若不正确，请举反例．

查看习题详情和答案>>

如图，直径AB、CD相互垂直，P为

上任意一点，连PC、PA、PD、PB，下列结论：
①∠APC=∠DPE；
②∠AED=∠DFA；
③

其中正确的是（　　）

查看习题详情和答案>>

正方形ABCD中，点O是对角线AC的中点，P是对角线AC上一动点，过点P作PF⊥CD于点F．如图1，当点P与点O重合时，显然有DF=CF．
（1）如图2，若点P在线段AO上（不与点A、O重合），PE⊥PB且PE交CD于点E．
①求证：DF=EF；
②写出线段PC、PA、CE之间的一个等量关系，并证明你的结论；
（2）若点P在线段OC上（不与点O、C重合），PE⊥PB且PE交直线CD于点E．请完成图3并判断（1）中的结论①、②是否分别成立？若不成立，写出相应的结论．（所写结论均不必证明）

查看习题详情和答案>>