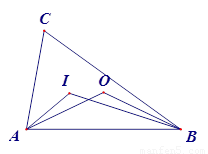
摘要： 解:(1)∠AOB=360°÷12=30° (2)在Rt△BOD中.∠AOB=30°.∴BD=OB=28. ∴S△OAB=×OA×BD=×56×28=784(cm2)
网址：http://m.1010jiajiao.com/timu3_id_465611[举报]
已知：如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，过O点作EF∥A
D分别交AB，CD于点E，F．
（1）下面是小明对“△AOB与△DOC是否相似”的解答：
解：△AOB∽△DOC理由如下：
∵AD∥BC（ ）
∴△AOD∽△COB
∴
=
（ ）
又∵∠AOB=∠DOC（ ）
∴△AOB∽△DOC（ ）
你认为小明的每一步解答过程是否正确？若正确，请在括号内填上理由；若不正确，请在该步骤后面的括号内打“×”．
（2）OE与OF有何关系？为什么？
（3）试求出
+
的值．
查看习题详情和答案>>
D分别交AB，CD于点E，F．（1）下面是小明对“△AOB与△DOC是否相似”的解答：
解：△AOB∽△DOC理由如下：
∵AD∥BC（ ）
∴△AOD∽△COB
∴
| OA |
| OC |
| OD |
| OB |
又∵∠AOB=∠DOC（ ）
∴△AOB∽△DOC（ ）
你认为小明的每一步解答过程是否正确？若正确，请在括号内填上理由；若不正确，请在该步骤后面的括号内打“×”．
（2）OE与OF有何关系？为什么？
（3）试求出
| OE |
| AD |
| OF |
| BC |
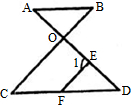22、已知：如图，AB∥CD，EF∥BC，∠AOB=70°；∠1+∠C=150°，求∠B的度数．解：∵∠AOB=70°，∴∠COD=∠
AOB
=70
°．∵EF∥BC，
∴∠COD+∠1=
180
°．∴∠1=
110
°．又∵∠1+∠C=150°，
∴∠C=150°-∠1=
40
°．∵AB∥CD，
∴∠B=∠
C
=40
°．
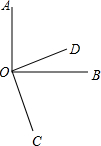补完下列解题过程：如图，已知∠AOB=90°，∠BOC=60°，OD平分∠AOC．求∠BOD的度数．
解：∵∠AOB=90°，∠BOC=60°，
∴∠AOC=∠AOB+∠BOC=
∵OD平分∠AOC，
∴∠AOD=∠COD=
| 1 | 2 |
∴∠BOD=∠AOB-∠AOD=
如图，点I和O分别是△ABC的内心和外心，则∠AIB和∠AOB的关系为( )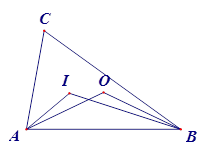
| A．∠AIB=∠AOB | B．∠AIB≠∠AOB |
| C．4∠AIB-∠AOB=360° | D．2∠AOB-∠AIB=180° |
