摘要:已知:关于x的方程有两个不相等的实数根和.并且抛物线与x轴的两个交点分别位于点(2.0)的两旁. (1)求实数a的取值范围, (2)当时.求a的值. [解](1)解法一:∵关于x的方程有两个不相等的实数根 解得:.且 设抛物线与x轴的两个交点的坐标分别为..且 ∴α.β是关于x的方程的两个不相等的实数根 ∴a为任意实数 <2> 由根与系数关系得: ∵抛物线与x轴的两个交点分别位于点(2.0)的两旁 解得: 由<1>.<2>.<3>得 a的取值范围是 解法二:同解法一.得:.且 ∵抛物线与x轴的两个交点分别位于点(2.0)两旁.且抛物线的开口向上 ∴当时. 解得: 由<1>.<2>得 a的取值范围是 (2)解:∵和是关于x的方程的两个不相等的实数根 不妨设 .即 解这个方程.得: 经检验.都是方程的根 .舍去 为所求
网址:http://m.1010jiajiao.com/timu3_id_459359[举报]
已知:关于![]() 的方程
的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
1.求![]() 的取值范围;
的取值范围;
2.抛物线![]() :
:![]() 与
与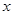 轴交于
轴交于![]() 、
、![]() 两点.若
两点.若![]() 且直线
且直线![]() :
:![]() 经过点
经过点![]() ,求抛物线
,求抛物线![]() 的函数解析式;
的函数解析式;
3.在(2)的条件下,直线![]() :
:![]() 绕着点
绕着点![]() 旋转得到直线
旋转得到直线![]() :
:![]() ,设直线
,设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线
,与抛物线![]() 交于点
交于点![]() (
(![]() 不与点
不与点![]() 重合),当
重合),当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看习题详情和答案>>
已知:关于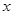 的方程
的方程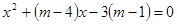 有两个不相等的实数根.
有两个不相等的实数根.
【小题1】求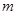 的取值范围;
的取值范围;
【小题2】抛物线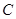 :
: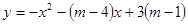 与
与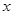 轴交于
轴交于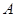 、
、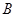 两点.若
两点.若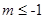 且直线
且直线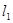 :
: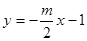 经过点
经过点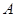 ,求抛物线
,求抛物线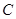 的函数解析式;
的函数解析式;
【小题3】在(2)的条件下,直线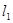 :
: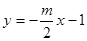 绕着点
绕着点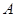 旋转得到直线
旋转得到直线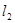 :
: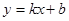 ,设直线
,设直线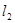 与
与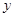 轴交于点
轴交于点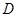 ,与抛物线
,与抛物线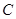 交于点
交于点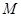 (
(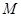 不与点
不与点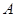 重合),当
重合),当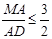 时,求
时,求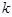 的取值范围.
查看习题详情和答案>>
的取值范围.
查看习题详情和答案>>
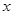 的方程
的方程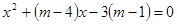 有两个不相等的实数根.
有两个不相等的实数根.【小题1】求
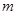 的取值范围;
的取值范围;【小题2】抛物线
 :
: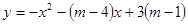 与
与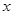 轴交于
轴交于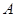 、
、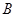 两点.若
两点.若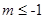 且直线
且直线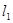 :
: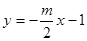 经过点
经过点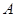 ,求抛物线
,求抛物线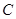 的函数解析式;
的函数解析式;【小题3】在(2)的条件下,直线
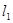 :
: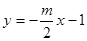 绕着点
绕着点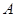 旋转得到直线
旋转得到直线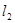 :
: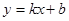 ,设直线
,设直线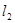 与
与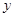 轴交于点
轴交于点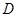 ,与抛物线
,与抛物线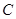 交于点
交于点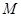 (
(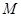 不与点
不与点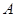 重合),当
重合),当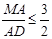 时,求
时,求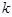 的取值范围.
查看习题详情和答案>>
的取值范围.
查看习题详情和答案>>
已知:关于 的方程
的方程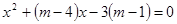 有两个不相等的实数根.
有两个不相等的实数根.
【小题1】求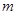 的取值范围;
的取值范围;
【小题2】抛物线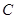 :
: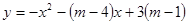 与
与 轴交于
轴交于 、
、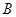 两点.若
两点.若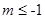 且直线
且直线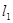 :
: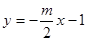 经过点
经过点 ,求抛物线
,求抛物线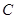 的函数解析式;
的函数解析式;
【小题3】在(2)的条件下,直线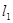 :
: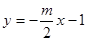 绕着点
绕着点 旋转得到直线
旋转得到直线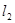 :
: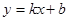 ,设直线
,设直线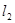 与
与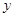 轴交于点
轴交于点 ,与抛物线
,与抛物线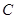 交于点
交于点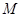 (
(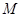 不与点
不与点 重合),当
重合),当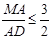 时,求
时,求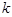 的取值范围.
的取值范围.
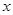 的方程
的方程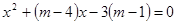 有两个不相等的实数根.
有两个不相等的实数根.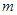 的取值范围;
的取值范围;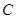 :
: 与
与 、
、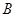 两点.若
两点.若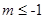 且直线
且直线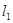 :
: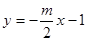 经过点
经过点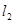 :
: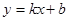 ,设直线
,设直线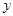 轴交于点
轴交于点 ,与抛物线
,与抛物线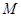 (
( 时,求
时,求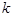 的取值范围.
的取值范围.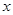 的方程
的方程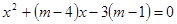 有两个不相等的实数根.
有两个不相等的实数根.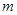 的取值范围;
的取值范围;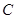 :
: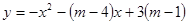 与
与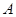 、
、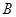 两点.若
两点.若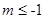 且直线
且直线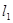 :
: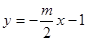 经过点
经过点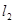 :
: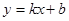 ,设直线
,设直线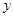 轴交于点
轴交于点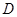 ,与抛物线
,与抛物线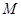 (
( 时,求
时,求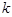 的取值范围.
的取值范围.