摘要:(1)1. (2)或 (3) (4) (3)解直角三角形
网址:http://m.1010jiajiao.com/timu3_id_458200[举报]
关于直角三角形的可解条件,在直角三角形的六个元素中,除直角外,只要再知道( )(其中至少( )),这个三角形的形状、大小就可以确定下来。解直角三角形的基本类型可分为已知两条边(两条( )或斜边和( ))及已知一边和一个锐角(( )和一个锐角或( )和一个锐角)。
查看习题详情和答案>>
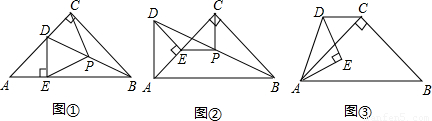
两个等腰直角三角形ABC,ADE,如图①摆放(E点在AB上),连BD,取BD的中点P,连PC、PE,则有PC=PE,PC⊥PE.
(1)将△ADE绕点A逆时针方向旋转,使E点落在AC上,如图②,结论是否仍成立?请证明你的判断.如果你经过反复探索,没有找到解决问题的办法,可通过连接AP,延长PE或延长DE,延长AD,延长BC的途径来完成你的证明.
(2)如图③,当△ADE绕点A逆时针方向旋转30°时,连DC,若DC∥AB,求 的值.
的值.

查看习题详情和答案>>
两个等腰直角三角形ABC,ADE,如图①摆放(E点在AB上),连BD,取BD的中点P,连PC、PE,则有PC=PE,PC⊥PE.
(1)将△ADE绕点A逆时针方向旋转,使E点落在AC上,如图②,结论是否仍成立?请证明你的判断.如果你经过反复探索,没有找到解决问题的办法,可通过连接AP,延长PE或延长DE,延长AD,延长BC的途径来完成你的证明.
(2)如图③,当△ADE绕点A逆时针方向旋转30°时,连DC,若DC∥AB,求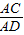 的值.
的值.
查看习题详情和答案>>
(1)将△ADE绕点A逆时针方向旋转,使E点落在AC上,如图②,结论是否仍成立?请证明你的判断.如果你经过反复探索,没有找到解决问题的办法,可通过连接AP,延长PE或延长DE,延长AD,延长BC的途径来完成你的证明.
(2)如图③,当△ADE绕点A逆时针方向旋转30°时,连DC,若DC∥AB,求
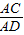 的值.
的值.
查看习题详情和答案>>
 在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3,1).
在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3,1).(1)求点B的坐标:
(2)求过A,O,B三点的抛物线的解析式;
(3)设点C为抛物线上的一点,且A、B、C、O可以构成梯形的四个顶点,请直接写出点C的坐标
(4,22)或(-2,-1)或(-4,
)
| 14 |
| 3 |
(4,22)或(-2,-1)或(-4,
)
.| 14 |
| 3 |
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时AP•CQ的值为
答:
(2)在(1)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2、图3供解题用)
(3)在(1)的条件下,PQ能否与AC平行?若能,求出y的值;若不能,试说明理由.

查看习题详情和答案>>
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时AP•CQ的值为
8
8
.将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,则AP•CQ的值是否会改变?答:
不会
不会
.(填“会”或“不会”)此时AP•CQ的值为8
8
.(不必说明理由)(2)在(1)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2、图3供解题用)
(3)在(1)的条件下,PQ能否与AC平行?若能,求出y的值;若不能,试说明理由.
