摘要:(1)连结DB.则∠DBO=90° ∵AB切⊙O于点C∵.AB⊥OD.又OD是⊙O’直径.即OA=OB 得OA2=OC·OD=r·2R=2Rr.即OA·OB=2rR (2)无变化 连结00'.并延长交⊙O'于D点.连结DB.OC. 证明△OCA∽△OBD.得OA·OB=OC·OD=r·2R=2Rr (3)无变化 连结00’.并延长交⊙O’于B点.连结DB.OC 证出△OCA∽△OBD.得OA·OB=OC·OD.:r·2R=2Rr
网址:http://m.1010jiajiao.com/timu3_id_457998[举报]
(7分)阅读材料,解答问题:
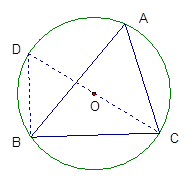
命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,ΔABC的外接圆半径为R,
则 2R.
2R. 
证明:连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,因为CD是⊙O的直径,所以∠DBC=900,在Rt△DBC中,sinD= ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  2R.
2R.
请阅读前面所给的命题和证明后,完成下面(1)(2)两题:
【小题1】(1)前面阅读材料中省略了“ ”的证明过程,请你把“
”的证明过程,请你把“ ”的证明过程补写出来.
”的证明过程补写出来.
【小题2】(2)直接运用阅读材料中命题的结论解题:已知锐角△ABC中, BC= ,CA=
,CA= ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.
(7分)阅读材料,解答问题:
命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,ΔABC的外接圆半径为R,
则 2R.
2R.

证明:连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,因为CD是⊙O的直径,所以∠DBC=900,在Rt△DBC中,sinD= ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  2R.
2R.
请阅读前面所给的命题和证明后,完成下面(1)(2)两题:
1.(1)前面阅读材料中省略了“ ”的证明过程,请你把“
”的证明过程,请你把“ ”的证明过程补写出来.
”的证明过程补写出来.
2.(2)直接运用阅读材料中命题的结论解题:已知锐角△ABC中, BC= ,CA=
,CA= ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.
查看习题详情和答案>>
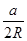 ,即
,即 2R.
2R. 
 ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  ”的证明过程补写出来.
”的证明过程补写出来.  ,CA=
,CA=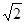 ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.