摘要:实数和数轴上的点是 对应的.每一个实数都可以用数轴上的 来表示.反过来.数轴上的点都表示一个 .
网址:http://m.1010jiajiao.com/timu3_id_457456[举报]
男、女运动员在100m直道的相对两端同时起跑,往返练习跑步,测得男运动员每百米跑12s,女运动员每百米跑15s,如上如图所示的实线和虚线分别为这两个运动员所跑路程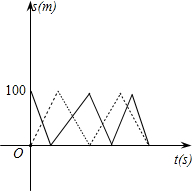 s(m)与时间t(s)之间的函数图象,请根据图象回答:
s(m)与时间t(s)之间的函数图象,请根据图象回答:
(1)在横轴的单位长度处填上相应的数字,从左至右依次为______;
(2)图中实线是______运动员跑步的图象,虚线是______运动员跑步的图象;
(3)在百米跑道的同一端点第一次相遇时,两人分别跑了______s,其中男运动员跑了______m,女运动员跑了______m;
(4)两运动员从开始起跑到第一次在同一端点相遇时共相遇了______次.
查看习题详情和答案>>
男、女运动员在100m直道的相对两端同时起跑,往返练习跑步,测得男运动员每百米跑12s,女运动员每百米跑15s,如上如图所示的实线和虚线分别为这两个运动员所跑路程
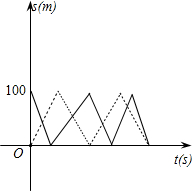
s(m)与时间t(s)之间的函数图象,请根据图象回答:
(1)在横轴的单位长度处填上相应的数字,从左至右依次为______;
(2)图中实线是______运动员跑步的图象,虚线是______运动员跑步的图象;
(3)在百米跑道的同一端点第一次相遇时,两人分别跑了______s,其中男运动员跑了______m,女运动员跑了______m;
(4)两运动员从开始起跑到第一次在同一端点相遇时共相遇了______次.
查看习题详情和答案>>

s(m)与时间t(s)之间的函数图象,请根据图象回答:
(1)在横轴的单位长度处填上相应的数字,从左至右依次为______;
(2)图中实线是______运动员跑步的图象,虚线是______运动员跑步的图象;
(3)在百米跑道的同一端点第一次相遇时,两人分别跑了______s,其中男运动员跑了______m,女运动员跑了______m;
(4)两运动员从开始起跑到第一次在同一端点相遇时共相遇了______次.
 九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.问题1:已知点A(m,1)在直线y=2x-1上,求m的方法是:
问题2:已知某个一次函数的图象经过点P(3,5)和Q(-4,-9),求这个一次函数的解析式时,一般先
(1999•河北)九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
问题1:已知点A(m,1)在直线y=2x-1上,求m的方法是: ,∴m= ;已知点B(-2,n)在直线y=2x-1上,求n的方法是: ,∴n= ;
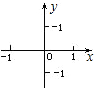
问题2:已知某个一次函数的图象经过点P(3,5)和Q(-4,-9),求这个一次函数的解析式时,一般先 ,再由已知条件可得 .解得: .∴满足已知条件的一次函数的解析式为: .这个一次函数的图象与两坐标轴的交点坐标为: ,在右侧给定的平面直角坐标系中,描出这两个点,并画出这个函数的图象.像解决问题2这样, 的方法,叫做待定系数法.
 查看习题详情和答案>>
查看习题详情和答案>>
问题1:已知点A(m,1)在直线y=2x-1上,求m的方法是: ,∴m= ;已知点B(-2,n)在直线y=2x-1上,求n的方法是: ,∴n= ;
问题2:已知某个一次函数的图象经过点P(3,5)和Q(-4,-9),求这个一次函数的解析式时,一般先 ,再由已知条件可得 .解得: .∴满足已知条件的一次函数的解析式为: .这个一次函数的图象与两坐标轴的交点坐标为: ,在右侧给定的平面直角坐标系中,描出这两个点,并画出这个函数的图象.像解决问题2这样, 的方法,叫做待定系数法.
 查看习题详情和答案>>
查看习题详情和答案>>