摘要：求证:y=x2+2mx-4(m-5)与x轴必有2个交点.
网址：http://m.1010jiajiao.com/timu3_id_457253[举报]
已知二次函数y=（n-1）x2+2mx+1图象的顶点在x轴上，
（1）试判断这个二次函数图象的开口方向，并说明你的理由；
（2）求证：函数y=m2x2+2（n-1）x-1的图象与x轴必有两个不同的交点． 查看习题详情和答案>>
（1）试判断这个二次函数图象的开口方向，并说明你的理由；
（2）求证：函数y=m2x2+2（n-1）x-1的图象与x轴必有两个不同的交点． 查看习题详情和答案>>
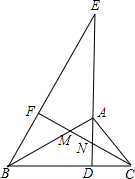已知，如图，AD为Rt△ABC斜边BC上的高，点E为DA延长线上一点，连接BE，过点C作CF⊥BE于点F，交AB、AD于M、N两点．（1）若线段AM、AN的长是关于x的一元二次方程x2-2mx+n2-mn+
| 5 |
| 4 |
（2）若AN=
| 15 |
| 8 |
| 9 |
| 8 |
（3）若在（1）的条件下，S△AMN：S△ABE=9：64，且线段BF与EF的长是关于y的一元二次方程5y2-16ky+10k2+5=0的两个实数根，求BC的长． 查看习题详情和答案>>
（2012•丰台区一模）已知：关于x的一元二次方程：x2-2mx+m2-4=0．
（1）求证：这个方程有两个不相等的实数根；
（2）当抛物线y=x2-2mx+m2-4与x轴的交点位于原点的两侧，且到原点的距离相等时，求此抛物线的解析式；
（3）将（2）中的抛物线在x轴下方的部分沿x轴翻折，其余部分保持能够不变，得到图形C1，将图形C1向右平移一个单位，得到图形C2，当直线y=x+b（b＜1）与图形C2恰有两个公共点时，写出b的取值范围．
查看习题详情和答案>>
（1）求证：这个方程有两个不相等的实数根；
（2）当抛物线y=x2-2mx+m2-4与x轴的交点位于原点的两侧，且到原点的距离相等时，求此抛物线的解析式；
（3）将（2）中的抛物线在x轴下方的部分沿x轴翻折，其余部分保持能够不变，得到图形C1，将图形C1向右平移一个单位，得到图形C2，当直线y=x+b（b＜1）与图形C2恰有两个公共点时，写出b的取值范围．
如图，已知：抛物线y1=x2-2mx+1，y2=-x2-2mx-1，CE、DF分别是抛物线y1、y2的对称轴．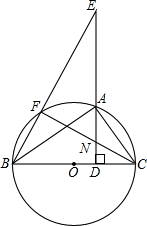
（2012•成都模拟）已知：如图，△ABC内接于⊙O，BC为直径，AD⊥BC于点D，点E为DA延长线上一点，连接BE，交⊙O于点F，连接CF，交AB、AD于M、N两点．