摘要:如图.在边长为2个单位长度的正方形ABCD中.点O.E分别是AD.AB的中点.点F是以点O为圆心.OE的长为半径的圆弧与DC的交点.点P是上的动点.连结OP.并延长交直线BC于点. (1)当点P从点E沿运动到点F时.点运动了多少个单位长度? (2)过点P作所在圆的切线.当该切线不与BC平行时.设它与射线AB.直线BC分别 交于点M.G. ①当K与B重合时.BG∶BM的值是多少? ②在点P运动的过程中.是否存在BG∶BM=3的情况?你若认为存在.请求出BK的值,你若认为不存在.试说明其中的理由. 一般地.是否存在BG∶BM=n的情况?试提出你的猜想. 例2如图.在矩形ABCD中.AB=6米.BC=8米.动点P以2米/秒的速度从点A出发.沿AC向点C移动.同时动点Q以1米/秒的速度从点C出发.沿CB向点B移动.设P.Q两点移动t秒后.四边形ABQP的面积为S米2. (1)求面积S与时间t的关系式, (2)在P.Q两点移动的过程中.四边形ABQP与△CPQ的面积能否相等?若能.求出此时点P的位置,若不能.请说明理由. 分析:本题是一个动态几何问题.也是一个数形结合的典型问题.综合性较强. 解: 设秒后, 的面积是的面积的一半, 则, 根据题意, 列出方程 , 化简, 得, 解得. 所以2秒和12秒均符合题意; (2) 当时, 在中, 作于, 在和中, , 所以; 当时, 同理可求得. 说明:本题考查的知识点较多.考查了勾股定理.平行线分线段成比例定理.一元二次方程及一元二次方程及根的判别式. 练习二
网址:http://m.1010jiajiao.com/timu3_id_455460[举报]
如图,在边长为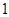 个单位长度的小正方形组成的网格中,小明家可用坐标
个单位长度的小正方形组成的网格中,小明家可用坐标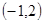 表示,汽车站可用坐标
表示,汽车站可用坐标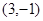 表示.
表示.
(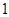 )建立平面直角坐标系,画出
)建立平面直角坐标系,画出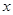 轴和
轴和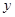 轴.(
轴.( 分)
分)
(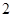 )某星期日早晨,小明同学从家出发,沿
)某星期日早晨,小明同学从家出发,沿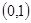
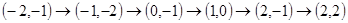 的路线转了一圈,又回到家里,写出他路上经过的地方;(
的路线转了一圈,又回到家里,写出他路上经过的地方;( 分)
分)
( )连接他在上一问中经过的地点,你得到了什么图形?(
)连接他在上一问中经过的地点,你得到了什么图形?( 分)
分)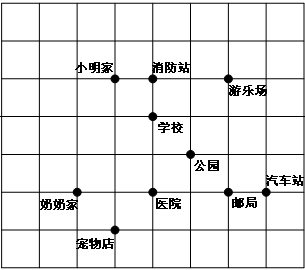 查看习题详情和答案>>
查看习题详情和答案>>
 个单位长度的小正方形组成的网格中,小明家可用坐标
个单位长度的小正方形组成的网格中,小明家可用坐标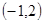 表示,汽车站可用坐标
表示,汽车站可用坐标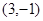 表示.
表示.(
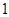 )建立平面直角坐标系,画出
)建立平面直角坐标系,画出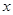 轴和
轴和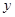 轴.(
轴.( 分)
分)(
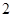 )某星期日早晨,小明同学从家出发,沿
)某星期日早晨,小明同学从家出发,沿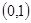
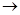
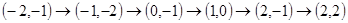 的路线转了一圈,又回到家里,写出他路上经过的地方;(
的路线转了一圈,又回到家里,写出他路上经过的地方;( 分)
分)(
 )连接他在上一问中经过的地点,你得到了什么图形?(
)连接他在上一问中经过的地点,你得到了什么图形?( 分)
分) 查看习题详情和答案>>
查看习题详情和答案>>
 个单位长度的小正方形组成的网格中,已知
个单位长度的小正方形组成的网格中,已知 ,分别探讨下面三个图形中
,分别探讨下面三个图形中 与
与 、
、 的关系,请任选一个加以说明.(
的关系,请任选一个加以说明.( 分)
分)


 ) (
) ( )
) 个单位长度的小正方形组成的网格中,已知
个单位长度的小正方形组成的网格中,已知 ,分别探讨下面三个图形中
,分别探讨下面三个图形中 与
与 、
、 的关系,请任选一个加以说明.(
的关系,请任选一个加以说明.( 分)
分)


 )
(
)
( )
) 个单位长度的小正方形组成的网格中,小明家可用坐标
个单位长度的小正方形组成的网格中,小明家可用坐标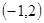 表示,汽车站可用坐标
表示,汽车站可用坐标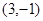 表示.
表示.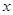 轴和
轴和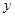 轴.(
轴.(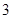 分)
分)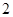 )某星期日早晨,小明同学从家出发,沿
)某星期日早晨,小明同学从家出发,沿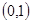
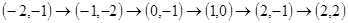 的路线转了一圈,又回到家里,写出他路上经过的地方;(
的路线转了一圈,又回到家里,写出他路上经过的地方;(
 个单位长度的小正方形组成的网格中,小明家可用坐标
个单位长度的小正方形组成的网格中,小明家可用坐标 表示,汽车站可用坐标
表示,汽车站可用坐标 表示。
表示。