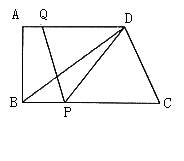
摘要:如图.在直角梯形ABCD中.AD∥BC.∠C=90°.BC=16.DC=12.AD=21.动点P从点D出发.沿射线DA的方向以每秒2两个单位长的速度运动.动点Q从点C出发.在线段CB上以每秒1个单位长的速度向点B运动.点P.Q分别从点D.C同时出发.当点Q运动到点B时.点P随之停止运动.设运动的时间为t(秒). (1)设△BPQ的面积为S.求S与t之间的函数关系式, (2)当t为何值时.以B.P.Q三点为顶点的三角形是等腰三角形? (3)当线段PQ与线段AB相交于点O.且2AO=OB时.求∠BQP的正切值, (4)是否存在时刻t.使得PQ⊥BD?若存在.求出t的值,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_455459[举报]
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21。动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动。设运动的时间为t(秒).
1.设△BPQ的面积为S,求S与t之间的函数关系式
2.当线段PQ与线段AB相交于点O,且2AO=OB时,求t的值.
3.当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
4.是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.

查看习题详情和答案>>