摘要:9.旋转的运用 例9 如图,△ABC和△ADE都是等腰直角三角形,∠C和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度? 解: 是旋转中心, 方向旋转了 . 基础达标
网址:http://m.1010jiajiao.com/timu3_id_455198[举报]
(1)观察发现
如图(1):若点A、B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:
作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
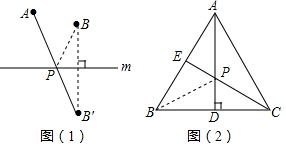
如图(2):在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:
作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为______.
(2)实践运用
如图(3):已知⊙O的直径CD为2, 的度数为60°,点B是
的度数为60°,点B是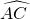 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为______.
的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为______.
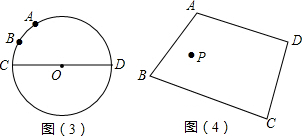
(3)拓展延伸
如图(4):点P是四边形ABCD内一点,分别在边AB、BC上作出点M,点N,使PM+PN+MN的值最小,保留作图痕迹,不写作法.
查看习题详情和答案>>
在直角梯形ABCD中,AD∥BC,∠B=∠A=90°.
操作示例
小明取直角梯形ABCD的非直角腰CD的中点P,过点P作PE∥AB,剪下△PEC(如图1),并将△PEC绕点P按逆时针方向旋转180°到△PFD的位置,拼成新的图形(如图2).
(Ⅰ)思考与实践:
(1)操作后小明发现,拼成的新图形是矩形,请帮他说明理由;
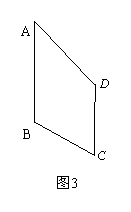
(2)类比图2的剪拼方法,请你在图3画出剪拼成一个平行四边形的示意图.
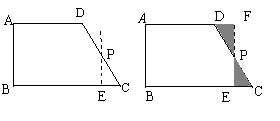 |
图1 图2
(Ⅱ)发现与运用:
小白发现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.
请你选择下面两题中的一题作答:(多做不加分,两题都做按第一题计分)

图4
(1)如图4,在梯形ABCD中,AD∥BC,E是CD的中点, EF⊥AB于点F,AB=5,EF=4,求梯形ABCD的面积。
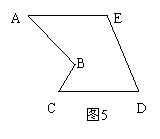
(2)如图5的多边形中,AE=CD,AE∥CD,能否沿一条直线进行剪切,拼成一个平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.
 |
查看习题详情和答案>>
在平面内,先将一个多边形以点![]() 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为![]() ,并且原多边形上的任一点
,并且原多边形上的任一点![]() ,它的对应点
,它的对应点![]() 在线段
在线段![]() 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点![]() 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度![]() ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为![]() ,其中点
,其中点![]() 叫做旋转相似中心,
叫做旋转相似中心,![]() 叫做相似比,
叫做相似比,![]() 叫做旋转角.
叫做旋转角.
(1
)填空:①如图1,将
②如图2,![]() 是边长为
是边长为![]() 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换![]() ,得到
,得到![]() ,则线段
,则线段![]() 的长为
的长为 ![]() ;
;
(2
)如图3,分别以锐角三角形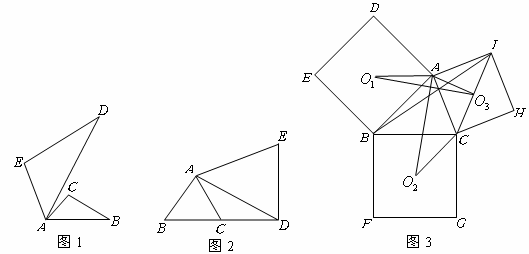
 7、如图,是2006年5月份的日历表,如图那样,用一个圈竖着圈住3个数,当你任意圈出一竖列上相邻的三个数时,请你运用方程思想来研究,发现这三个数的和不可能是( )
7、如图,是2006年5月份的日历表,如图那样,用一个圈竖着圈住3个数,当你任意圈出一竖列上相邻的三个数时,请你运用方程思想来研究,发现这三个数的和不可能是( )