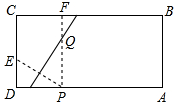
摘要:16.如图.矩形纸片ABCD中.AB=3 cm.BC=4 cm.现将A.C重合.使纸片 折叠压平.设折痕为EF.试求AF的长和重叠部分△AEF的面积. [提示]把AF取作△AEF的底.AF边上的高等于AB=3. 由折叠过程知.EF经过矩形的对称中心.FD=BE.AE=CE=AF.由此可以在 △ABE中使用勾股定理求AE.即求得AF的长. [答案]如图.连结AC.交EF于点O. 由折叠过程可知.OA=OC. ∴ O点为矩形的对称中心.E.F关于O点对称.B.D也关于O点对称. ∴ BE=FD.EC=AF. 由EC折叠后与EA重合. ∴ EC=EA. 设AF=x.则BE=FD=AD-AF=4-x.AE=AF=x. 在Rt△ABE中.由勾股定理.得 AB2+BE2=AE2.即 32+(4-x) 2=x2. 解得 x=. ∴ S△AEF=×3×=(cm2) 故AF的长为cm.△AEF的面积为cm2.
网址:http://m.1010jiajiao.com/timu3_id_455178[举报]
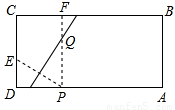
如图,矩形纸片ABCD中,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,AD上有一点P,PD=3cm,过点P作PF⊥AD交BC于点F,将纸片折叠,使P与E重合,折痕交PF于Q,则线段PQ的长是 cm.
查看习题详情和答案>>
如图,矩形纸片ABCD中,AB=5cm,BC=10cm,CD上有一点E,EC=2cm,AD上有一点P,PA=6cm,过点P作PF⊥AD交BC于点F,将纸片折叠,使P与E重合,折痕交PF于Q,则线段PQ的长是( )cm.
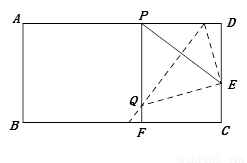
A.4
B.4.5 C. 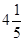 D.
D.
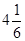
查看习题详情和答案>>
如图,矩形纸片ABCD中,AB=5cm,BC=10cm,E、P分别为CD、DA边上的点,ED=2cm,PD=3cm, PF⊥AD,折叠纸片,使P点与E点重合,折痕与PF交于Q点,则PQ的长是____________cm.

查看习题详情和答案>>