摘要:已知:如图.在△ABC中.AB=AC.AD⊥BC.垂足为点D.AN是△ABC外角∠CAM的平分线.CE⊥AN.垂足为点E. (1)求证:四边形ADCE为矩形, (2)当△ABC满足什么条件时.四边形 ADCE是一个正方形?并给出证明. (1)证明:在△A BC中. AB=AC.AD⊥BC. ∴ ∠BAD=∠DAC. ------------1分 ∵ AN是△ABC外角∠CAM的平分线. ∴ .----------------2分 ∴ ∠DAE=∠DAC+∠CAE=180°=90°.-----3分 又 ∵ AD⊥BC.CE⊥AN. ∴ =90°. ------------4分 ∴ 四边形ADCE为矩形. ------------5分 (2)说明:给出正确条件得1分.证明正确得2分. 例如.当AD=时.四边形ADCE是正方形.----6分 证明:∵ AB=AC.AD⊥BC于D. ∴ DC=. ---------------7分 又 AD=.∴ DC=AD. 由(1)四边形ADCE为矩形. ∴ 矩形ADCE是正方形.
网址:http://m.1010jiajiao.com/timu3_id_455115[举报]
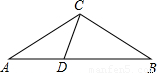
(2007•淄博)已知:如图,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB•AD.
(1)试说明:△ADC和△BDC都是等腰三角形;(2)若AB=1,求AC的值;
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)
 查看习题详情和答案>>
查看习题详情和答案>>
(1)试说明:△ADC和△BDC都是等腰三角形;(2)若AB=1,求AC的值;
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)
 查看习题详情和答案>>
查看习题详情和答案>>
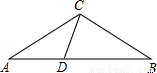
(2007•淄博)已知:如图,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB•AD.
(1)试说明:△ADC和△BDC都是等腰三角形;(2)若AB=1,求AC的值;
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)
 查看习题详情和答案>>
查看习题详情和答案>>
(1)试说明:△ADC和△BDC都是等腰三角形;(2)若AB=1,求AC的值;
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)
 查看习题详情和答案>>
查看习题详情和答案>>
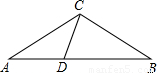
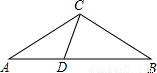
(2007•淄博)已知:如图,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB•AD.
(1)试说明:△ADC和△BDC都是等腰三角形;(2)若AB=1,求AC的值;
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)
 查看习题详情和答案>>
查看习题详情和答案>>
(1)试说明:△ADC和△BDC都是等腰三角形;(2)若AB=1,求AC的值;
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)
 查看习题详情和答案>>
查看习题详情和答案>>