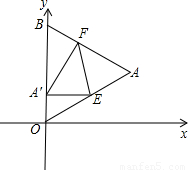
摘要:如图.△OAB是边长为的等边三角形.其中O是坐标原点.顶点B在轴正方向上.将△OAB 折叠.使点A落在边OB上.记为A′.折痕为EF. (1)当A′E//轴时.求点A′和E的坐标, (2)当A′E//轴.且抛物线经过点A′和E时.求抛物线与轴的交点的坐标, (3) 当点A′在OB上运动.但不与点O.B重合时.能否使△A′EF成为直角三角形?若能.请求出此时点A′的坐标,若不能.请你说明理由. [解析](1)由已知可得∠A.OE=60o , A.E=AE 由A′E//轴,得△OA.E是直角三角形. 设A.的坐标为(0.b) AE=A.E=,OE=2b 所以b=1.A..E的坐标分别是(0.1)与(.1) (2) 因为A..E在抛物线上.所以 所以.函数关系式为 由得 与x轴的两个交点坐标分别是(.0)与(.0) (3) 不可能使△A′EF成为直角三角形. ∵∠FA.E=∠FAE=60o,若△A′EF成为直角三角形,只能是∠A.EF=90o或∠A.FE=90o 若∠A.EF=90o,利用对称性,则∠AEF=90o, A..E.A三点共线.O与A重合.与已知矛盾, 同理若∠A.FE=90o也不可能 所以不能使△A′EF成为直角三角形.
网址:http://m.1010jiajiao.com/timu3_id_454632[举报]
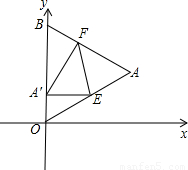
(2006•临安市)如图,△OAB是边长为2+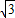 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E∥x轴时,求点A′和E的坐标;
(2)当A′E∥x轴,且抛物线y=- x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
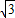 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.(1)当A′E∥x轴时,求点A′和E的坐标;
(2)当A′E∥x轴,且抛物线y=-
 x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(2006•临安市)如图,△OAB是边长为2+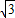 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E∥x轴时,求点A′和E的坐标;
(2)当A′E∥x轴,且抛物线y=- x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
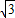 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.(1)当A′E∥x轴时,求点A′和E的坐标;
(2)当A′E∥x轴,且抛物线y=-
 x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF. x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;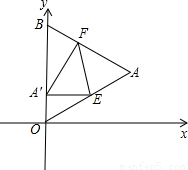
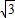 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF. x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;