摘要：17． 如图14().两个不全等的等腰直角三角形和叠放在一起.并且有公共的直角顶点． (1)将图14()中的绕点顺时针旋转角.在图14()中作出旋转后的(保留作图痕迹.不写作法.不证明)． (2)在图14()中.你发现线段.的数量关系是 .直线.相交成 度角． (3)将图14()中的绕点顺时针旋转一个锐角.得到图14().这时(2)中的两个结论是否成立?作出判断并说明理由．若绕点继续旋转更大的角时.结论仍然成立吗?作出判断.不必说明理由．
网址：http://m.1010jiajiao.com/timu3_id_450958[举报]
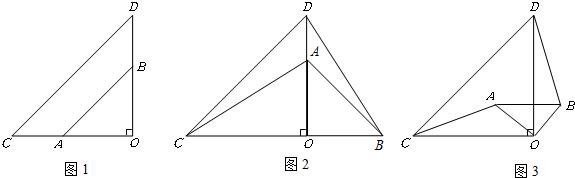
30、如图1，两个不全等的等腰直角三角形OAB和OCD叠放在一起，并且有公共的直角顶点O．
（1）在图1中，你发现线段AC、BD的数量关系是
（2）将图1的△OAB绕点O顺时针旋转90°角，在图2中画出旋转后的△OAB．
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，连接AC、BD得到图3，这时（1）中的两个结论是否成立？作出判断并说明理由．若△OAB绕点O继续旋转更大的角时，结论仍然成立吗？作出判断，不必说明理由．
查看习题详情和答案>>
（1）在图1中，你发现线段AC、BD的数量关系是
相等
；直线AC、BD相交成角的度数是90°
．（2）将图1的△OAB绕点O顺时针旋转90°角，在图2中画出旋转后的△OAB．
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，连接AC、BD得到图3，这时（1）中的两个结论是否成立？作出判断并说明理由．若△OAB绕点O继续旋转更大的角时，结论仍然成立吗？作出判断，不必说明理由．
如图1，两个不全等的等腰直角三角形OAB和OCD叠放在一起，并且有公共的直角顶点O．
（1）在图1中，你发现线段AC，BD的数量关系是
（2）将图1中的△OAB绕点O顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出判断并说明理由．
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．
解：（2）在图2中，（1）中的两个结论
理由如下：延长CA交BD于点
（2）在图3中，（1）中的两个结论
理由如下：延长CA交BD于点
查看习题详情和答案>>
（1）在图1中，你发现线段AC，BD的数量关系是
相等
相等
，直线AC，BD相交成90
90
度角．（2）将图1中的△OAB绕点O顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出判断并说明理由．
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．
解：（2）在图2中，（1）中的两个结论
成立
成立
（是否成立）；理由如下：延长CA交BD于点
E，∵等腰直角三角形OAB和OCD，
∴OA=OB，OC=OD，
∵AC2=AO2+CO2，BD2=OD2+OB2，
∴AC=BD；
∴△DOB≌△COA（SSS），
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°，则∠AEB=90°，即直线AC，BD相交成90°角．
∴OA=OB，OC=OD，
∵AC2=AO2+CO2，BD2=OD2+OB2，
∴AC=BD；
∴△DOB≌△COA（SSS），
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°，则∠AEB=90°，即直线AC，BD相交成90°角．
E，∵等腰直角三角形OAB和OCD，
∴OA=OB，OC=OD，
∵AC2=AO2+CO2，BD2=OD2+OB2，
∴AC=BD；
∴△DOB≌△COA（SSS），
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°，则∠AEB=90°，即直线AC，BD相交成90°角．
；∴OA=OB，OC=OD，
∵AC2=AO2+CO2，BD2=OD2+OB2，
∴AC=BD；
∴△DOB≌△COA（SSS），
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°，则∠AEB=90°，即直线AC，BD相交成90°角．
（2）在图3中，（1）中的两个结论
成立
成立
（是否成立）；理由如下：延长CA交BD于点
F
F
，交OD于点E
E
．29、如图1，两个不全等的等腰直角三角形OAB和OCD叠放在一起，并且有公共的直角顶点O．
（1）在图1中，你发现线段AC，BD的数量关系是
（2）将图1中的△OAB绕点O顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出判断并说明理由．
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．
查看习题详情和答案>>
（1）在图1中，你发现线段AC，BD的数量关系是
相等
，直线AC，BD相交成90
度角．（2）将图1中的△OAB绕点O顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出判断并说明理由．
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．
27、如图1，两个不全等的四边形ABCD、四边形CGFE是正方形，连接BG，DE．交DC于H，交CG于K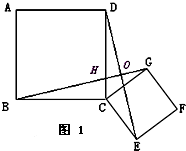
（1）观察图形，①猜想BG与DE之间长度关系；②猜想BG与DE所在直线的位置关系，并证明你的猜想．
直接回答：连接四边形DBEG四边中点所得四边形是
（2）如图2，将原题中正方形改为菱形，且∠BCD=∠GCE=90°．则（1）中的①、②的结论是否成立？若成立，请证明；若不成立，请说明理由．
直接回答：连接四边形DBEG四边中点所得四边形是
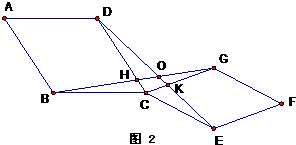
（3）如图3，将原题中正方形改为矩形，且BC=mCG、CD=mCE则（1）中的①、②结论是否成立？不要证明
直接回答：连接四边形DBEG四边中点所得四边形是
查看习题详情和答案>>
（1）观察图形，①猜想BG与DE之间长度关系；②猜想BG与DE所在直线的位置关系，并证明你的猜想．
直接回答：连接四边形DBEG四边中点所得四边形是
正方
形（2）如图2，将原题中正方形改为菱形，且∠BCD=∠GCE=90°．则（1）中的①、②的结论是否成立？若成立，请证明；若不成立，请说明理由．
直接回答：连接四边形DBEG四边中点所得四边形是
正方
形（3）如图3，将原题中正方形改为矩形，且BC=mCG、CD=mCE则（1）中的①、②结论是否成立？不要证明
直接回答：连接四边形DBEG四边中点所得四边形是
矩
形．
和
叠放在一起，并且有公共的直角顶点
．
，
的数量关系是 ，直线
绕点
角，这时（1）中的两个结论是否成立？请做出判断并说明理由．