摘要：28．解(1)抛物线过. ·········································································································· 1分 点在抛物线上. . 点的坐标为．·················································································· 3分 得. .. ．······························································································· 6分 (3)的面积有最大值.············································································ 7分 的对称轴为.. 点的坐标为.··················································································· 8分 由(1)得. 而 .······························································································ 10分 的对称轴是. 当时.取最大值. 其最大值为． 12分
网址：http://m.1010jiajiao.com/timu3_id_450913[举报]
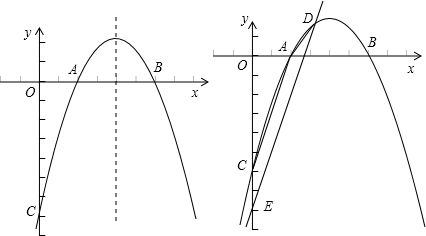
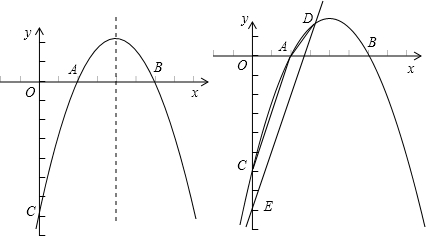
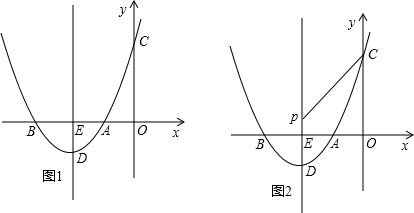
抛物线y=ax2-4ax+b经过A（1，0），F（4，-3），与y轴交于点C，与x轴交于另一点B．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上是否存在一点P，连接PC，将线段PC绕着P点逆时针旋转90°至线段PC1，使得C1落在抛物线上？若存在，求点P的坐标；若不存在，请说明理由；
（3）点D是抛物线在x轴上方部分的一点，过D作DE∥AC与y轴交于E，且四边形ACED是等腰梯形，求出D的坐标．
查看习题详情和答案>>
（1）求抛物线的解析式；
（2）在抛物线的对称轴上是否存在一点P，连接PC，将线段PC绕着P点逆时针旋转90°至线段PC1，使得C1落在抛物线上？若存在，求点P的坐标；若不存在，请说明理由；
（3）点D是抛物线在x轴上方部分的一点，过D作DE∥AC与y轴交于E，且四边形ACED是等腰梯形，求出D的坐标．
查看习题详情和答案>>
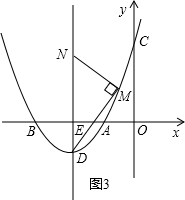
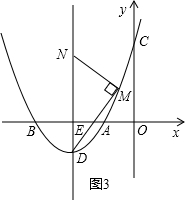
抛物线y=a（x+6）2-3与x轴相交于A，B两点，与y轴相交于C，D为抛物线的顶点，直线DE⊥x轴，垂足为E，AE2=3DE．
（1）求这个抛物线的解析式；
（2）P为直线DE上的一动点，以PC为斜边构造直角三角形，使直角顶点落在x轴上．若在x轴上的直角顶点只有一个时，求点P的坐标；
（3）M为抛物线上的一动点，过M作直线MN⊥DM，交直线DE于N，当M点在抛物线的第二象限的部分上运动时，是否存在使点E三等分线段DN的情况？若存在，请求出所有符合条件的M的坐标；若不存在，请说明理由．
查看习题详情和答案>>
（1）求这个抛物线的解析式；
（2）P为直线DE上的一动点，以PC为斜边构造直角三角形，使直角顶点落在x轴上．若在x轴上的直角顶点只有一个时，求点P的坐标；
（3）M为抛物线上的一动点，过M作直线MN⊥DM，交直线DE于N，当M点在抛物线的第二象限的部分上运动时，是否存在使点E三等分线段DN的情况？若存在，请求出所有符合条件的M的坐标；若不存在，请说明理由．
查看习题详情和答案>>
抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
（1）根据上表填空：
①抛物线与x轴的交点坐标是
②抛物线经过点 （-3，
③在对称轴右侧，y随x增大而
（2）试确定抛物线y=ax2+bx+c的解析式．
查看习题详情和答案>>
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | -4 | -4 | 0 | 8 | … |
①抛物线与x轴的交点坐标是
（-2，0）
（-2，0）
和（1，0）
（1，0）
；②抛物线经过点 （-3，
8
8
）；③在对称轴右侧，y随x增大而
增大
增大
；（2）试确定抛物线y=ax2+bx+c的解析式．
