摘要:(二)选择填空 1.已知:点O是ΔABC的外心,∠A=,则∠BOC等于: A.2 B.360°-2 C.2或360°-2 D.180°-2 2.在⊙O中,AB=2CD,则AB与CD的关系是: A.AB=2CD B.AB>2CD C.CD<AB<2CD D.不确定 3.在ΔAOB中,∠O=90°,以OB为半径的⊙O分别交AB,AO与C,D.∠A=28°,则CD的度数是: A.28° B.56° C.62° D.34° 4.ΔABC内接于⊙O,OD⊥BC于D,∠BOD=38°,则∠A等于: A.19° B.38°或142° C.19°或161° D.38° 5.在⊙O中,两条直径AB⊥CD于O,弦AP交CD于Q,则AP·AQ等于: A.AO·OB B.CQ·QD C.AO·AB D.OQ·BP (三)证明题 1.ΔABC中,∠A的平分线交BC于D.交 ΔABC外接圆于E.∠ABC的平分线交AD于F. 求证:BE=EF. 2.已知在ΔABC中,∠A的内,外角平分线 分别交ΔABC的外接圆于D,E. 求证:DE垂直平分BC. 3.AB是⊙O的直径,弦CD⊥AB,M是AC 上一点,延长AM,DC交于N. 求证:∠AMD=∠NMC
网址:http://m.1010jiajiao.com/timu3_id_450224[举报]
阅读下面材料并填空:
已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|,当A、B两点都不在原点时,
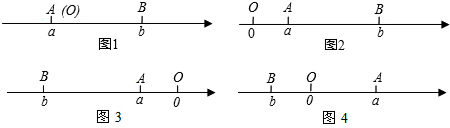
(1)如图2,点A、B都在原点的右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
(2)如图3,点A、B在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=a-b=|a-b|;
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=a-b=|a-b|.
综上,数轴上A、B两点的距离|AB|=|a-b|.
利用上述结论,小明同学这样解决了以下问题:
数轴上表示x和-1的两点之间的距离是|x+1|,表示x和2的两点之间的距离是|x-2|,当x的取值范围为-1≤x≤2时,代数式|x+1|+|x-2|取最小值3.并且他发现:对于代数式|x-a1|+|x-a2|+…+|x-an|,当n为奇数时,把a1,a2,…an从小到大排列,x等于最中间的数值时,原式值最小;当n为偶数时,把a1,a2,…an从小到大排列,x取最中间两个数值之间的数(包括最中间的两个数)时,原式值最小.
请你仿照小明的方法解决下面问题(也可以考虑其他方法):
若y=|1-x|+|2-3x|+|3-4x|+|4-5x|+|5-6x|+|6-7x|,则当x的取值范围是
≤x≤
≤x≤
时,y取最小值
.
查看习题详情和答案>>
已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|,当A、B两点都不在原点时,

(1)如图2,点A、B都在原点的右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
(2)如图3,点A、B在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=a-b=|a-b|;
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=a-b=|a-b|.
综上,数轴上A、B两点的距离|AB|=|a-b|.
利用上述结论,小明同学这样解决了以下问题:
数轴上表示x和-1的两点之间的距离是|x+1|,表示x和2的两点之间的距离是|x-2|,当x的取值范围为-1≤x≤2时,代数式|x+1|+|x-2|取最小值3.并且他发现:对于代数式|x-a1|+|x-a2|+…+|x-an|,当n为奇数时,把a1,a2,…an从小到大排列,x等于最中间的数值时,原式值最小;当n为偶数时,把a1,a2,…an从小到大排列,x取最中间两个数值之间的数(包括最中间的两个数)时,原式值最小.
请你仿照小明的方法解决下面问题(也可以考虑其他方法):
若y=|1-x|+|2-3x|+|3-4x|+|4-5x|+|5-6x|+|6-7x|,则当x的取值范围是
| 3 |
| 4 |
| 6 |
| 7 |
| 3 |
| 4 |
| 6 |
| 7 |
| 4 |
| 3 |
| 4 |
| 3 |
阅读下面材料并填空:
已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|,当A、B两点都不在原点时,

(1)如图2,点A、B都在原点的右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
(2)如图3,点A、B在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=a-b=|a-b|;
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=a-b=|a-b|.
综上,数轴上A、B两点的距离|AB|=|a-b|.
利用上述结论,小明同学这样解决了以下问题:
数轴上表示x和-1的两点之间的距离是|x+1|,表示x和2的两点之间的距离是|x-2|,当x的取值范围为-1≤x≤2时,代数式|x+1|+|x-2|取最小值3.并且他发现:对于代数式|x-a1|+|x-a2|+…+|x-an|,当n为奇数时,把a1,a2,…an从小到大排列,x等于最中间的数值时,原式值最小;当n为偶数时,把a1,a2,…an从小到大排列,x取最中间两个数值之间的数(包括最中间的两个数)时,原式值最小.
请你仿照小明的方法解决下面问题(也可以考虑其他方法):
若y=|1-x|+|2-3x|+|3-4x|+|4-5x|+|5-6x|+|6-7x|,则当x的取值范围是______时,y取最小值______.
查看习题详情和答案>>
已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|,当A、B两点都不在原点时,

(1)如图2,点A、B都在原点的右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
(2)如图3,点A、B在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=a-b=|a-b|;
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=a-b=|a-b|.
综上,数轴上A、B两点的距离|AB|=|a-b|.
利用上述结论,小明同学这样解决了以下问题:
数轴上表示x和-1的两点之间的距离是|x+1|,表示x和2的两点之间的距离是|x-2|,当x的取值范围为-1≤x≤2时,代数式|x+1|+|x-2|取最小值3.并且他发现:对于代数式|x-a1|+|x-a2|+…+|x-an|,当n为奇数时,把a1,a2,…an从小到大排列,x等于最中间的数值时,原式值最小;当n为偶数时,把a1,a2,…an从小到大排列,x取最中间两个数值之间的数(包括最中间的两个数)时,原式值最小.
请你仿照小明的方法解决下面问题(也可以考虑其他方法):
若y=|1-x|+|2-3x|+|3-4x|+|4-5x|+|5-6x|+|6-7x|,则当x的取值范围是______时,y取最小值______.

