摘要：例1:解方程组 x2+y2＝25 -① 4x-3y＝0 -② 分析: (1)这是一个由一个二元一次方程和一个二元二次方程组成的二元二次方程组.与解二元一次方程组类似.可以用代入法来解. (2)方程②是一个二元一次方程.把这个方程变形为.就可把未知数x用未知数y的代数式来表示. (3)把代入方程①.即可消去未知数x.得到一个关于y的一元二次方程.解这个方程即可得y的值.再把y的值代入.就可求出未知数x的值.从而得到方程组的解. 解:由②得: -③ 把③代入①得.()2+y2＝25 解这个方程得:y1＝4, y2＝-4 把y1代入③得:x1＝3 把y2代入③得:x2＝-3 ∴原方程组的解为: x1＝3 x1＝-3 y1＝4. y1＝-4, 例2:解方程组 x+y＝12 -① xy＝7 -② 由①得:x＝12-y -③ 把③代入②得:y＝7 即:y2-12y+7=0 解得: 把代入③得: 把代入③得: ∴原方程组的解为 . , 根据一元二次方程根与系数的关系 可把x.y看成一元二次方程的两根 解得, ∴原方程组的解为 . , 例3:解方程组 -① xy＝12 -② :①+2×②得:(x+y)2＝49 ∴x+y＝±7 -③ ①-2×②得:(x-y)2＝1 ∴x-y＝±1 -④ 由③④可组成以下四个二元一次方程组 x+y＝7 x+y＝7 x+y＝-7 x+y＝-7 x-y＝1 x-y＝-1 x-y＝1 x-y＝-1 解这四个方程组得原方程组的解为:x1＝4 x2＝3 x3＝-3 x4＝-4 y1＝3 y2＝4 y3＝-4 y4＝-3 :①+2×②得:(x+y)2＝49 ∴x+y＝±7 -③ 由②③可组成以下两个方程组: x+y＝7 和 x+y＝-7 xy＝12 xy＝12 以下如例2的.分别解出这两个方程组可得出原方程组的四组解 由②得.代入①消去x可得关于y的特殊的四次方程.用换元法解得y的各值再分别代入即可求得原方程组的四组解(只写了思路.具体解题过程略) 由②得:.令u＝x2.v＝y2 则有 u+v＝25 再如例2的求出u.v,最后再求出原方程组的四组解. (只写了思路.具体解题过程略) 例4. 解方程组 -① -② 解:由①得 ∴ ∴原方程组可化为以下两个方程组: 分别解这两个方程组得原方程组的解为 x1＝4 x2＝-4 x3＝-3 x4＝4 y1＝3 y2＝-3 y3＝4 y4＝-3 例5:解方程组: -① -② 解:由①得: ∴x-y＝±3 由②得:=0 即:x+2y+2=0或x+2y-1=0 ∴原方程组可化为以下四个方程组: x-y=3 x-y=3 x-y=-3 x-y=-3 x+2y+2=0 x+2y-1=0 x+2y+2=0 x+2y-1=0 解这四个方程组.得原方程组的解为: 例题注释:解二元二次方程组的基本思想方法是“降次 和“消元 .初中阶段主要是熟练掌握由一个二元一次方程和一个二元二次方程组成的方程组的解法.由一个二元二次方程和一个可以分解为两个二元一次方程的方程组成的方程组的解法.前者由上述例1.例2说明用代入消元法解,后者由上述例3.例4.例5说明用降次化为几个二元一次方程组或前者形式的方程再消元求解.有一种常用的降次方法是利用分解二次多项式为两个一次式乘积而把一个二元二次方程化为两个二元一次方程的.这种降次方法一定要熟悉.对其它的降次方法如例3的.也需了解并能使用.例2的是利用根与系数关系构造一新未知数的一元二次方程求解的简便方法.对此特殊解法也需熟悉.总之.消元和降次是数学中两种重要的常见的转化方法.利用消元可把多元转化为少元.通过降次能把高次转化为低次.

网址：http://m.1010jiajiao.com/timu3_id_449638[举报]
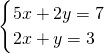
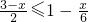