摘要：已知.如图⊙P与⊙0相交于点A.B.并且⊙P经过点O.点C是⊙P的优弧AB上任意一点.弦OC交公共弦AB于点D.连结CA.CB. (1)求证:CD·CO=CA·CB (2)当点C在⊙P上什么位置时.直线CA与⊙O相切?并说明理由, (3)当∠ACB等于60°时.两圆的半径有什么关系?并说明理由. (1)如图.OA.OB是⊙O的两条半径.且OA⊥OB.点C是OB延长线上任意一点:过点C作CD切⊙O于点D.连结AD交DC于点E．求证:CD=CE (2)若将图8中的半径OB所在直线向上平行移动交OA于F.交⊙O于B’.其他条件不变.那么上述结论CD=CE还成立吗?为什么? (3)若将图8中的半径OB所在直线向上平行移动到⊙O外的CF.点E是DA的延长线与CF的交点.其他条件不变.那么上述结论CD=CE还成立吗?为什么
网址：http://m.1010jiajiao.com/timu3_id_449154[举报]
已知：如图，抛物线C1：交y轴交于点B，交x轴于点A、E（点E在点A的右边）．且连接AB=
，cot∠ABO=3，Q（-2，-5）在C1上．
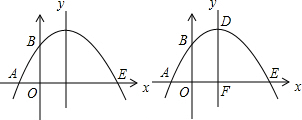
（1）求抛物线C1的解析式；
（2）若一个动点P自OB的中点H出发，先到达x轴上某点（设为N），再到达抛物线的对称轴上某点（设为点K）最后到达点B，求使点P运动的总路径最短的点N，点K的坐标，并求出这个最短总路径的长；
（3）设抛物线C1的对称轴与x轴交于点F，顶点为D，另一条抛物线C2经过点E（抛物线C2与抛物线C1不重合）且顶点为M（a，b）b＜0，对称轴与x轴相交于点G，且以M、G、E为顶点的三角形与以D、E、F为顶点的三角形全等，求a、b的值（只需写结果，不必写出解答过程）
查看习题详情和答案>>
已知：如图所示，直线l的解析式为
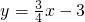，并且与x轴、y轴分别交于点A、B．
（1）求A、B两点的坐标；
（2）半径为0.75的⊙O1，以0.4个单位/秒的速度从原点向x轴正方向运动，问在什么时刻与直线l相切；
（3）在第（2）题的条件下，在⊙O1运动的同时，与之大小相同的⊙O2从点B出发，沿BA方向运动，两圆经过的区域重叠部分是什么形状的图形？并求出其面积．
查看习题详情和答案>>
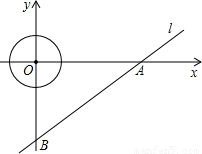
已知：如图所示，直线l的解析式为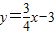
，并且与x轴、y轴分别交于点A、B．
（1）求A、B两点的坐标；
（2）半径为0.75的⊙O1，以0.4个单位/秒的速度从原点向x轴正方向运动，问在什么时刻与直线l相切；
（3）在第（2）题的条件下，在⊙O1运动的同时，与之大小相同的⊙O2从点B出发，沿BA方向运动，两圆经过的区域重叠部分是什么形状的图形？并求出其面积．
查看习题详情和答案>>
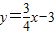，并且与x轴、y轴分别交于点A、B．（1）求A、B两点的坐标；
（2）半径为0.75的⊙O1，以0.4个单位/秒的速度从原点向x轴正方向运动，问在什么时刻与直线l相切；
（3）在第（2）题的条件下，在⊙O1运动的同时，与之大小相同的⊙O2从点B出发，沿BA方向运动，两圆经过的区域重叠部分是什么形状的图形？并求出其面积．
查看习题详情和答案>>
x2＋bx＋c经过点C，且与x轴交于D、E两点，A点在此抛物线的对称轴上．
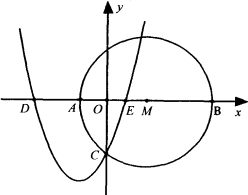
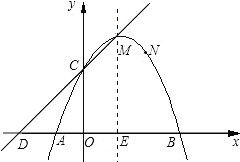的P点，使以P为圆心的圆经过A、B两点，并且与直线CD相切？若存在，请求出点P的坐标；若不存在，请说明理由．