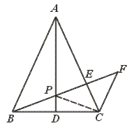
摘要：28．已知:如图.△ABC中.AB＝AC.AD是中线.P是AD上一点.过C作CF∥AB.延长BP交AC于E.交CF于F．求证:BP2＝PE·PF． [提示]先证PB＝PC.再证△EPC∽△CPF． [答案]连结PC． ∵ AB＝AC.AD是中线.∴ AD是△ABC的对称轴． ∴ PC＝PB.∠PCE＝∠ABP．∵ CF∥AB. ∴ ∠PFC＝∠ABP．∴ ∠PCE＝∠PFC． 又 ∠CPE＝∠EPC.∴ △EPG∽△CPF． ∴ ＝．即 PC2＝PE·PF．∴ BP2＝PE·PF． [点评]本题要求运用等腰三角形的性质以及相似三角形的判定与性质．

网址：http://m.1010jiajiao.com/timu3_id_448898[举报]