摘要:27.已知:如图.在正方形ABCD中.P是BC上的点.且BP=3PC.Q是CD的中点.求证:△ADQ∽△QCP. [提示]先证=. [答案]在正方形ABCD中. ∵ Q是CD的中点.∴ =2. ∵ =3.∴ =4. 又 BC=2DQ.∴ =2. 在△ADQ和△QCP中.=.∠C=∠D=90°. ∴ △ADQ∽△QCP. [点评]本题要求运用相似三角形的判定定理.
网址:http://m.1010jiajiao.com/timu3_id_448897[举报]
 23、已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
23、已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.(1)求证:BE=DF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM,FM,判断四边形AEMF是什么特殊四边形?并证明你的结论.
已知:如图,在正方形ABCD中,AD=12,点E是边CD上的动点(点E不与端点C,D重合),AE的垂直平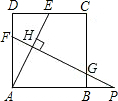 分线FP分别交AD,AE,BC于点F,H,G,交AB的延长线于点P.
分线FP分别交AD,AE,BC于点F,H,G,交AB的延长线于点P.
(1)设DE=m(0<m<12),试用含m的代数式表示
的值;
(2)在(1)的条件下,当
=
时,求BP的长.
查看习题详情和答案>>
 分线FP分别交AD,AE,BC于点F,H,G,交AB的延长线于点P.
分线FP分别交AD,AE,BC于点F,H,G,交AB的延长线于点P.(1)设DE=m(0<m<12),试用含m的代数式表示
| FH |
| HG |
(2)在(1)的条件下,当
| FH |
| HG |
| 1 |
| 2 |
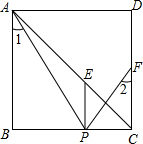 已知:如图,在正方形ABCD中,F是CD边上的中点,点P在BC上,∠1=∠2,PE⊥BC交AC于点E,垂足为P.求证:AB=3PE.
已知:如图,在正方形ABCD中,F是CD边上的中点,点P在BC上,∠1=∠2,PE⊥BC交AC于点E,垂足为P.求证:AB=3PE.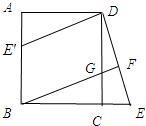 29、已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
29、已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.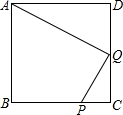 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?