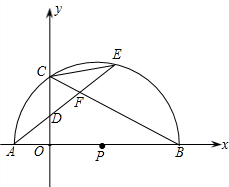
摘要：26．如图.P为轴正半轴上一点.半圆P交轴于A.B两点.交轴于C点.弦AE分别交OC.CB于点D.F.已知. (1)求证:AD＝CD, (2)若DF＝.tan∠ECB＝.求经过A.B.C三点的抛物线的解析式, (3)设M为轴负半轴上一点.OM＝AE.是否存在过点M的直线.使该直线与(2)中所得的抛物线的两个交点到轴距离相等?若存在.求出这条直线的解析式,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_447686[举报]
如图，在平面直角坐标系中，直线l：y=-2x-8分别与x轴，y轴相交于A，B两点，点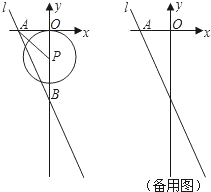
P（0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P．
（1）连接PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；
（2）当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形． 查看习题详情和答案>>
P（0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P．（1）连接PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；
（2）当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形． 查看习题详情和答案>>
如图，直角坐标系中，已知两点O（0，0），A（2，0），点B在第一象限且△OA
B为正三角形，△OAB的外接圆交y轴的正半轴于点C，过点C的圆的切线交x轴于点D．
（1）求B，C两点的坐标；
（2）求直线CD的函数解析式；
（3）设E，F分别是线段AB，AD上的两个动点，且EF平分四边形ABCD的周长．试探究：△AEF的最大面积． 查看习题详情和答案>>
B为正三角形，△OAB的外接圆交y轴的正半轴于点C，过点C的圆的切线交x轴于点D．（1）求B，C两点的坐标；
（2）求直线CD的函数解析式；
（3）设E，F分别是线段AB，AD上的两个动点，且EF平分四边形ABCD的周长．试探究：△AEF的最大面积． 查看习题详情和答案>>
如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（ ）
| A、2.5 | ||
B、2
| ||
C、
| ||
D、
|
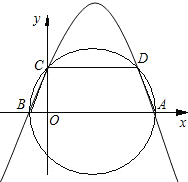的正半轴交于点C，以AB为直径的圆经过点C及抛物线上的另一点D，∠ABC=60度．
与（2）中所得的抛物线的两个交点到y轴距离相等？若存在，求出这条直线的解析式；若不存在，请说明理由．