摘要:6.①y=50x+45=5x+3600. ∵两种型号的时装共用A种布料[1.1x+0.6]米. 共用B种布料[0.4x+0.9]米. ∴ 解之得40≤x≤44. 而x为整数. ∴x=40.41.42.43.44. ∴y与x的函数关系式是y=5x+3600, ②∵y随x的增大而增大. ∴当x=44时.y最大=3820. 即生产M型号的时装44套时.该厂所获利润最大.最大利润是3820元.
网址:http://m.1010jiajiao.com/timu3_id_447446[举报]
【解题思路】通过读题、审题
(1)完成表格有2个思路:从供或需的角度考虑,均能完成上表。
(2)运用公式(调运水的重量×调运的距离)
总调运量=A的总调运量+B的总调运量调运水的重量×调运的距离
y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275(注:一次函数的最值要得到自变量的取值范围)∵5>0∴y随x的增大而增大,y要最小则x应最大
由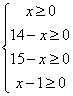 解得1≤x≤14
解得1≤x≤14
y=5x+1275中∵5>0∴y随x的增大而增大,y要最小则x应最小=1
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
【答案】⑴(从左至右,从上至下)14-x 15-x x-1
⑵y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275
解不等式1≤x≤14
所以x=1时y取得最小值
y=5+1275=1280
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
查看习题详情和答案>>解方程
(
x-30)=7,下列变形较简便的是( )
| 4 |
| 5 |
| 5 |
| 4 |
| A、方程两边都乘以20,得4(5x-120)=140 | ||||||
B、方程两边都除以
| ||||||
| C、去括号,得x-24=7 | ||||||
D、方程整理,得
|