摘要:如图.在中...动点从点出发沿边向点以每秒个单位长的速度运动.动点从点出发沿边向点以每秒个单位长的速度运动.分别从点同时出发.当其中一点到达端点时.另一点也随之停止运动.在运动过程中.关于直线对称的图形是.设运动时间为(秒). (1)设四边形的面积为.求与的函数关系式, (2)为何值时.四边形是梯形? (3)是否存在时刻.使得?若存在.求出的值,若不存在.请说明理由, (4)通过观察.画图或折纸等方法.猜想是否存在时刻.使得?若存在.请估计的值在括号中的哪个时间段内(,,,),若不存在.请简要说明理由. 答案:解:(1)由题意知.. . 与关于直线对称. .-- (2)当时.有.而与不平行.这时四边形是梯形.. .解得. 当秒时.四边形是梯形. -- (3)设存在时刻.使得.延长交于点.如图2. 若.则.又. .从而. .. . 若.则.得. 解得. 当秒时.. -- (4)存在时刻.使得.-- 时间段为:. .如果考生通过计算得到当时..也给2分)
网址:http://m.1010jiajiao.com/timu3_id_447401[举报]
如图,在梯形![]() 中,
中,![]() 动点
动点![]() 从
从![]() 点出发沿线段
点出发沿线段![]() 以每秒2个单位长度的速度向终点
以每秒2个单位长度的速度向终点![]() 运动;动点
运动;动点![]() 同时从
同时从![]() 点出发沿线段
点出发沿线段![]() 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点![]() 运动.设运动的时间为
运动.设运动的时间为![]() 秒.
秒.
(1)求![]() 的长.
的长.
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)试探究:![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
 |
查看习题详情和答案>>
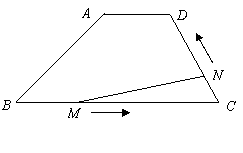
如图,在梯形![]() 中,
中,![]() 动点
动点![]() 从
从![]() 点出发沿线段
点出发沿线段![]() 以每秒2个单位长度的速度向终点
以每秒2个单位长度的速度向终点![]() 运动;动点
运动;动点![]() 同时从
同时从![]() 点出发沿线段
点出发沿线段![]() 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点![]() 运动.设运动的时间为
运动.设运动的时间为![]() 秒.
秒.
(1)求![]() 的长.
的长.
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)试探究:![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
 |
查看习题详情和答案>>
如图,在梯形![]() 中,
中,![]() 动点
动点![]() 从
从![]() 点出发沿线段
点出发沿线段![]() 以每秒2个单位长度的速度向终点
以每秒2个单位长度的速度向终点![]() 运动;动点
运动;动点![]() 同时从
同时从![]() 点出发沿线段
点出发沿线段![]() 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点![]() 运动.设运动的时间为
运动.设运动的时间为![]() 秒.
秒.
(1)求![]() 的长.
的长.
(2)当![]() 时
时![]() ,求
,求![]() 的值.
的值.
(3)试探![]() 究:
究:![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
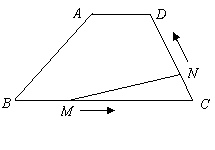
 中,
中, ,
, ,
, ,动点
,动点 从点
从点 开始沿边
开始沿边 向
向 以
以 的速度移动(不与点
的速度移动(不与点 从点
从点 向
向 以
以 的速度移动(不与点
的速度移动(不与点 的面积最小.
的面积最小.
 中,
中, ,
, ,
, ,
, 分别是边
分别是边 的中点,点
的中点,点 从点
从点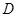 出发沿
出发沿 方向运动,过点
方向运动,过点 于
于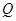 ,过点
,过点 交
交 于
于 ,当点
,当点 重合时,点
重合时,点 ,
, .
.
 的距离
的距离 的长;
的长; 关于
关于 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围); 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的