摘要:用数学归纳法证明+cosα+cos3α+-+cos(2n-1)α=·· (α≠kπ,n∈N*),验证n=1等式成立时,左边计算所得的项是( ) A. B.+cosα C.+cosα+cos3α D.+cosα+cos3α+cos5α 分析 分清等式左边的构成情况是解决此题的关键;对于本题也可把n=1代入右边化简得出左边. 解法一 因为等式的左边是(n+1)项的形式,故n=1时,应保留两项,它们是+cosα. 解法二 当n=1时,右边=sincos=·= (sinαcosα+sinα)=+cosα. 答案 B
网址:http://m.1010jiajiao.com/timu3_id_4473467[举报]
用数学归纳法证明 +cosα+cos3α+…+cos(2n-1)α=
+cosα+cos3α+…+cos(2n-1)α= ·
· ·
·
(α≠kπ,n∈N*),验证n=1等式成立时,左边计算所得的项是( )
A.![]() B.
B.![]() +cosα
+cosα
C.![]() +cosα+cos3α D.
+cosα+cos3α D.![]() +cosα+cos3α+cos5α
+cosα+cos3α+cos5α
用数学归纳法证明
+cosα+cos3α+…+cos(2n-1)α=
(k∈Z*,α≠kπ,n∈N+),在验证n=1时,左边计算所得的项是
+cosα
+cosα.
查看习题详情和答案>>
| 1 |
| 2 |
sin
| ||||
| sina |
| 1 |
| 2 |
| 1 |
| 2 |
 +cosα+cos3α+…+cos(2n-1)α=
+cosα+cos3α+…+cos(2n-1)α=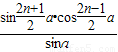 (k∈Z*,α≠kπ,n∈N+),在验证n=1时,左边计算所得的项是 .
(k∈Z*,α≠kπ,n∈N+),在验证n=1时,左边计算所得的项是 .