摘要：已知二次函数同时满足:①不等式的解集有且只有一个元素,②在定义域内存在.使得不等式成立. 设数列的前项和. (1)求数列的通项公式, (2)试构造一个数列.(写出的一个通项公式)满足:对任意的正整数都有.且.并说明理由, (3)设各项均不为零的数列中.所有满足的正整数的个数称为这个数列的变号数.令(为正整数).求数列的变号数. 解:(1)∵的解集有且只有一个元素.∴. 当时.函数在上递增.故不存在.使得不等式成立. 当时.函数在上递减.故存在.使得不等式成立. 综上.得..∴.∴ (2)要使.可构造数列.∵对任意的正整数都有. ∴当时.恒成立.即恒成立.即. 又.∴.∴.等等. (3)解法一:由题设. ∵时..∴时.数列递增. ∵.由.可知.即时.有且只有个变号数, 又∵.即.∴此处变号数有个. 综上得 数列共有个变号数.即变号数为. 解法二:由题设. 时.令, 又∵.∴时也有. 综上得 数列共有个变号数.即变号数为.
网址：http://m.1010jiajiao.com/timu3_id_4471014[举报]
已知二次函数
同时满足：⑴不等式
的解集有且只有一个元素；⑵在定义域内存在
，使得不等式
成立。设数列
的前
（1）求数列的通项公式；
（2）设
（3）设各项均不为零的数列
中，所有满足
的正整数i的个数称为这个数列的变号数.另
已知二次函数
同时满足：⑴不等式
的解集有且只有一个元素；⑵在定义域内存在
，使得不等式
成立。设数列
的前
（1）求数列的通项公式；
（2）设
（3）设各项均不为零的数列
中，所有满足
的正整数i的个数称为这个数列的变号数.另
同时满足：①不等式
的解集有且只有一个元素；②在定义域内存在
，使得不等式
成立。设数列
的前n项和
。（1）求
的解析式；（2）求数列
，
，
前n项和为
，
（
恒成立，求实数m的取值范围.
同时满足：
的解集有且只有一个元素；
，使得不等式
成立.
的通项公式为
.
的表达式； 
项和
.
同时满足：①不等式
的解集有且只有一个元素；②在定义域内存在
，使得不等式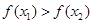
成立,设数列
的前
项和
。
的表达式；
的数列
中，所有满足
的整数
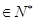的个数称为这个数列
（
）,求数列