摘要：16．设F1.F2分别为椭圆C: =1(a＞b＞0)的左.右两个焦点.(1)若椭圆C上的点A(1.)到F1.F2两点的距离之和等于4.写出椭圆C的方程和焦点坐标, 中所得椭圆上的动点.求线段F1K的中点的轨迹方程.
网址：http://m.1010jiajiao.com/timu3_id_4470765[举报]
设F1、F2分别为椭圆C：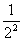
=1(A＞b＞0)的左、右两个焦点.
=1(A＞b＞0)的左、右两个焦点.（1）若椭圆C上的点A（1，3[]2）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标;
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程;
（3）已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM?,kPN时，那么kPM与kPN之积是与点P位置无关的定值，试写出双曲线
=1具有类似特性的性质并加以证明.
设F1、F2分别为椭圆C：
=1(A＞b＞0)的左、右两个焦点.
=1(A＞b＞0)的左、右两个焦点.（1）若椭圆C上的点A（1，3[]2）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标;
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程;
（3）已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM?,kPN时，那么kPM与kPN之积是与点P位置无关的定值，试写出双曲线
=1具有类似特性的性质并加以证明.
设F1、F2分别为椭圆C：
+
=1(a＞b＞0)的左、右两个焦点.
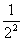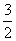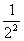+=1(a＞b＞0)的左、右两个焦点.（1）若椭圆C上的点A（1,
）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标.
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程.
（3）已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM、kPN时，那么kPM与kPN之积是与点P位置无关的定值，试写出双曲线
=1具有类似特性的性质并加以证明.
+
=1(a＞b＞0)的左、右两个焦点.
）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标.
=1具有类似特性的性质并加以证明.
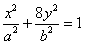（a＞b＞0）的左、右两个焦点。
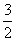）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标；
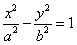写出具有类似特性的性质，并加以证明。