摘要:21. 设是函数的一个极值点. (Ⅰ).求与的关系式(用表示).并求的单调区间, (Ⅱ).设..若存在使得成立.求的取值范围. 点评:本小题主要考查函数.不等式和导数的应用等知识.考查综合运用数学知识解决问题的能力. 解:(Ⅰ)f `(x)=-[x2+(a-2)x+b-a ]e3-x, 由f `(3)=0.得 -[32+(a-2)3+b-a ]e3-3=0.即得b=-3-2a. 则 f `(x)=[x2+(a-2)x-3-2a-a ]e3-x =-[x2+(a-2)x-3-3a ]e3-x=-(x-3)(x+a+1)e3-x. 令f `(x)=0.得x1=3或x2=-a-1.由于x=3是极值点. 所以x+a+1≠0.那么a≠-4. 当a<-4时.x2>3=x1.则 在区间上.f `(x)<0. f (x)为减函数, 在区间(3.―a―1)上.f `(x)>0.f (x)为增函数, 在区间(―a―1.+∞)上.f `(x)<0.f (x)为减函数. 当a>-4时.x2<3=x1.则 在区间(-∞.―a―1)上.f `(x)<0. f (x)为减函数, 在区间(―a―1.3)上.f `(x)>0.f (x)为增函数, 在区间上.f `(x)<0.f (x)为减函数. 知.当a>0时.f (x)在区间(0.3)上的单调递增.在区间(3.4)上单调递减.那么f (x)在区间[0.4]上的值域是[min.f (4) ).f (3)]. 而f (0)=-(2a+3)e3<0.f (4)=(2a+13)e-1>0.f (3)=a+6. 那么f (x)在区间[0.4]上的值域是[-(2a+3)e3.a+6]. 又在区间[0.4]上是增函数. 且它在区间[0.4]上的值域是[a2+.(a2+)e4]. 由于(a2+)-(a+6)=a2-a+=()2≥0.所以只须仅须 (a2+)-(a+6)<1且a>0.解得0<a<. 故a的取值范围是(0.).
网址:http://m.1010jiajiao.com/timu3_id_4468896[举报]
(本小题满分14分)已知函数![]() (其中
(其中![]() 是自然对数的底数,
是自然对数的底数,![]() 为正数)
为正数)
(I)若![]() 在
在![]()
![]() 处取得极值,且
处取得极值,且![]() 是
是![]() 的一个零点,求
的一个零点,求![]() 的值;(II)若
的值;(II)若![]() ,求
,求![]() 在区间
在区间![]() 上的最大值;(III)设函数
上的最大值;(III)设函数![]() 在区间
在区间![]() 上是减函数,求
上是减函数,求![]() 的取值范围。
的取值范围。
 ,当
,当 时,
时, 取得极
取得极 小值
小值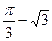 .
. ,
, 的值;
的值; ,曲线
,曲线 .若直线
.若直线
 与曲线
与曲线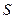 同时满足下列两个条件:
同时满足下列两个条件: 切点;
切点;  都有
都有 .则称直线
.则称直线 是曲线
是曲线 的“上夹线”.
的“上夹线”. ,设
,设 是方程
是方程 的实数
的实数 根,若对于
根,若对于 定义域中任意的
定义域中任意的 、
、 ,当
,当 ,且
,且 时,问是否存在一个最小的正整数
时,问是否存在一个最小的正整数 ,使得
,使得 恒成立,若存在请求出
恒成立,若存在请求出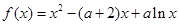 ,其中常数
,其中常数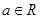 .
.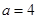 时,求函数
时,求函数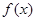 的极值点;
的极值点; ,若函数
,若函数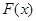 在区间
在区间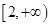 上单调递增,求
上单调递增,求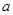 的取值范围;
的取值范围;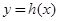 在点
在点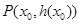 处的切线方程为
处的切线方程为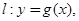 当
当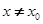 时,若
时,若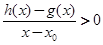 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数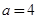 时,函数
时,函数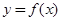 是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.
是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.