摘要:21. 设数列..满足:.(n=1,2,3,-). 证明:为等差数列的充分必要条件是为等差数列且(n=1,2,3,-) [考点分析:本题主要考查等差数列.充要条件等基础知识.考查综合运用数学知识分析问题和解决问题的能力] [证明]必要性:设数列是公差为的等差数列.则: ==-=0. ∴(n=1,2,3,-)成立, 又=6(n=1,2,3,-) ∴数列为等差数列. 充分性:设数列是公差为的等差数列.且(n=1,2,3,-). ∵--① ∴--② ①-②得:= ∵ ∴--③ 从而有--④ ④-③得:--⑤ ∵... ∴由⑤得:(n=1,2,3,-). 由此.不妨设(n=1,2,3,-).则 故--⑥ 从而--⑦ ⑦-⑥得:. 故(n=1,2,3,-). ∴数列为等差数列. 综上所述:为等差数列的充分必要条件是为等差数列且(n=1,2,3,-).
网址:http://m.1010jiajiao.com/timu3_id_4468773[举报]
(本小题满分14分)已知递增数列![]() 满足:
满足:![]() ,
,![]()
![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列。(I)求数列
成等比数列。(I)求数列![]() 的通项公式
的通项公式![]() ;(II)若数列
;(II)若数列![]() 满足:
满足:![]()
![]() ,且
,且![]() 。①证明数列
。①证明数列![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式
的通项公式![]() ;②设
;②设![]() ,数列
,数列![]() 前
前![]() 项和为
项和为![]() ,
,
![]() ,
,![]() 。当
。当![]() 时,试比较A与B的大小。
时,试比较A与B的大小。
(本小题满分14分)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,其中
,其中![]() 为常数,且
为常数,且![]() 、0.(1)证明:数列
、0.(1)证明:数列![]() 是等比数列;(2)设数列
是等比数列;(2)设数列![]() 的公比
的公比![]() ,数列
,数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;(3)设
的通项公式;(3)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() 时,
时,![]()
(本小题满分14分)已知递增数列![]() 满足:
满足:![]() ,
,![]()
![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列。(I)求数列
成等比数列。(I)求数列![]() 的通项公式
的通项公式![]() ;(II)若数列
;(II)若数列![]() 满足:
满足:![]()
![]() ,且
,且![]() 。①证明数列
。①证明数列![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式
的通项公式![]() ;②设
;②设![]() ,数列
,数列![]() 前
前![]() 项和为
项和为![]() ,
,
![]() ,
,![]() 。当
。当![]() 时,试比较A与B的大小。
时,试比较A与B的大小。
 上的函数
上的函数 ,满足条件:①
,满足条件:①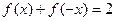 ,②对非零实数
,②对非零实数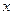 ,都有
,都有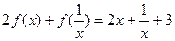 .
.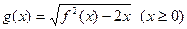 ,直线
,直线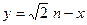 分别与函数
分别与函数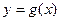 ,
,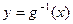 交于
交于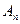 、
、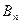 两点,(其中
两点,(其中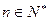 );设
);设 ,
,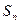 为数列
为数列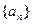 的前
的前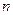 项和,求证:当
项和,求证:当 时,
时,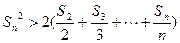 .
. ,当
,当 时,
时, 取得极
取得极 小值
小值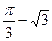 .
. ,
, 的值;
的值; ,曲线
,曲线 .若直线
.若直线
 与曲线
与曲线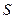 同时满足下列两个条件:
同时满足下列两个条件: 切点;
切点;  都有
都有 .则称直线
.则称直线 是曲线
是曲线 的“上夹线”.
的“上夹线”. ,设
,设 是方程
是方程 的实数
的实数 根,若对于
根,若对于 定义域中任意的
定义域中任意的 、
、 ,当
,当 ,且
,且 时,问是否存在一个最小的正整数
时,问是否存在一个最小的正整数 ,使得
,使得 恒成立,若存在请求出
恒成立,若存在请求出