摘要:解不等式:. 已知函数.求f(x)的定义域.判断它的奇偶性.并求其值域. 如图.正四棱柱ABCD-A1B1C1D1中.底面边长为.侧棱长为4.E.F分别为棱AB.BC的中点.. (Ⅰ)求证:平面B1EF⊥平面BDD1B1, (Ⅱ)求点D1到平面B1EF的距离d, (Ⅲ)求三棱锥B1-EFD1的体积V. 某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时.可全部租出.当每辆车的月租金每增加50元时.未租出的车将会增加一辆.租出的车每辆每月需要维护费150元.未租出的车每辆每月需要维护需50元. (Ⅰ)当每辆车的月租金定为3600元时.能租出多少辆车? (Ⅱ)当每辆车的月租金定为多少元时.租赁公司的月收益最大?最大月收益是多少? 如图.在边长为l的等边△ABC中.圆O1为△ABC的内切圆.圆O2与圆O1外切.且与AB.BC相切.-.圆On+1与圆On外切.且与AB.BC相切.如此无限继续下去.记圆On的面积为an(n∈N). (Ⅰ)证明{an}是等比数列, (Ⅱ)求的值. 已知动圆过定点P(1.0).且与定直线l:x=-1相切.点C在l上. (Ⅰ)求动圆圆心的轨迹M的方程, (Ⅱ)设过点P.且斜率为的直线与曲线M相交于A.B两点. (ⅰ)问:△ABC能否为正三角形?若能.求点C的坐标,若不能.说明理由, (ⅱ)当△ABC为钝角三角形时.求这种点C的纵坐标的取值范围. 普通高等学校春季招生考试
网址:http://m.1010jiajiao.com/timu3_id_4467964[举报]
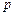 :关于
:关于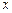 的不等式
的不等式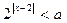 的解集为
的解集为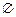 ;命题
;命题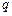 :函数
:函数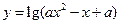 的值域是
的值域是 .如果命题
.如果命题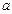 的取值范围.
的取值范围.