摘要：设三角形ABC的BC边上的高AD=BC.分别为其对应边.则的最大值为25.设F1和F2是双曲线 -y2=1 的两个焦点.点P在双曲线上.且满足∠F1PF2＝90°.则△F1PF2的面积是( ).
网址：http://m.1010jiajiao.com/timu3_id_4466816[举报]
已知△ABC的内角A，B，C的对边分别为a，b，c，下列说法中：①在△ABC中，a=x，b=2，B=45°，若该三角形有两解，则x取值范围是
；②在△ABC中，若b=8，c=5，A=60°，则△ABC的外接圆半径等于
；③在△ABC中，若c=5，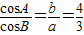
，则△ABC的内切圆的半径为2；④在△ABC中，若AB=4，AC=7，BC=9，则BC边的中线
；⑤设三角形ABC的BC边上的高AD=BC，a、b、c分别表示角A、B、C对应的三边，则
的取值范围是
．其中正确说法的序号是 （注：把你认为是正确的序号都填上）．
查看习题详情和答案>>
；②在△ABC中，若b=8，c=5，A=60°，则△ABC的外接圆半径等于；③在△ABC中，若c=5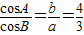，，则△ABC的内切圆的半径为2；④在△ABC中，若AB=4，AC=7，BC=9，则BC边的中线；⑤设三角形ABC的BC边上的高AD=BC，a、b、c分别表示角A、B、C对应的三边，则的取值范围是．其中正确说法的序号是 （注：把你认为是正确的序号都填上）．
查看习题详情和答案>>
已知△ABC的内角A，B，C的对边分别为a，b，c，下列说法中：①在△ABC中，a=x，b=2，B=45°，若该三角形有两解，则x取值范围是2＜x＜2
；②在△ABC中，若b=8，c=5，A=60°，则△ABC的外接圆半径等于
；③在△ABC中，若c=5，
=
=
，则△ABC的内切圆的半径为2；④在△ABC中，若AB=4，AC=7，BC=9，则BC边的中线AD=
；⑤设三角形ABC的BC边上的高AD=BC，a、b、c分别表示角A、B、C对应的三边，则
+
的取值范围是[2，
]．其中正确说法的序号是
查看习题详情和答案>>
| 2 |
14
| ||
| 3 |
| cosA |
| cosB |
| b |
| a |
| 4 |
| 3 |
| 7 |
| 2 |
| b |
| c |
| c |
| b |
| 5 |
①④⑤
①④⑤
（注：把你认为是正确的序号都填上）．已知△ABC的内角A，B，C的对边分别为a，b，c，下列说法中：①在△ABC中，a=x，b=2，B=45°，若该三角形有两解，则x取值范围是2＜x＜2
；②在△ABC中，若b=8，c=5，A=60°，则△ABC的外接圆半径等于
；③在△ABC中，若c=5，
=
=
，则△ABC的内切圆的半径为2；④在△ABC中，若AB=4，AC=7，BC=9，则BC边的中线AD=
；⑤设三角形ABC的BC边上的高AD=BC，a、b、c分别表示角A、B、C对应的三边，则
+
的取值范围是[2，
]．其中正确说法的序号是______（注：把你认为是正确的序号都填上）．
查看习题详情和答案>>
| 2 |
14
| ||
| 3 |
| cosA |
| cosB |
| b |
| a |
| 4 |
| 3 |
| 7 |
| 2 |
| b |
| c |
| c |
| b |
| 5 |