摘要：(理)函数≤x≤0)的反函数是 A.( 0≤x≤2) B.(0≤x≤2) C. ( 0≤x≤2) D. (0≤x≤2) (文)函数的反函数是 A. B. C. D.
网址：http://m.1010jiajiao.com/timu3_id_4465157[举报]
设函数f（x）的定义域、值域均为R，f（x）的反函数为f-1（x），且对于任意的x∈R，均有f(x)+f-1(x)＜
x，定义数列{an}，a0=8，a1=10，an=f（an-1）（n∈N*）．
（Ⅰ）求证：an+1+an-1＜
an（n∈N*）．
（Ⅱ）设bn=an+1-2an（n∈N*），求证：bn＜（-6）•2-n（n∈N*）；
（Ⅲ）是否存在常数A，B同时满足条件：
①当n=0，1时，an=
；
②当n≥2时（n∈N*，）an＜
．如果存在，求出A，B的值，如果不存在，说明理由．
查看习题详情和答案>>
| 5 |
| 2 |
（Ⅰ）求证：an+1+an-1＜
| 5 |
| 2 |
（Ⅱ）设bn=an+1-2an（n∈N*），求证：bn＜（-6）•2-n（n∈N*）；
（Ⅲ）是否存在常数A，B同时满足条件：
①当n=0，1时，an=
| A•4n+B |
| 2n |
②当n≥2时（n∈N*，）an＜
| A•4n+B |
| 2n |
设函数f（x）的定义域、值域均为R，f（x）的反函数为f-1（x），且对于任意的x∈R，均有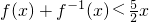
，定义数列{an}，a0=8，a1=10，an=f（an-1）（n∈N*）．
（Ⅰ）求证：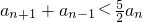
（n∈N*）．
（Ⅱ）设bn=an+1-2an（n∈N*），求证：bn＜（-6）•2-n（n∈N*）；
（Ⅲ）是否存在常数A，B同时满足条件：
①当n=0，1时，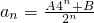
；
②当n≥2时（n∈N*，）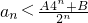
．如果存在，求出A，B的值，如果不存在，说明理由．
查看习题详情和答案>>
设函数f（x）的定义域、值域均为R，f（x）的反函数为f-1（x），且对于任意的x∈R，均有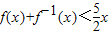
，定义数列{an}，a=8，a1=10，an=f（an-1）（n∈N*）．
（Ⅰ）求证：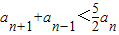
（n∈N*）．
（Ⅱ）设bn=an+1-2an（n∈N*），求证：bn＜（-6）•2-n（n∈N*）；
（Ⅲ）是否存在常数A，B同时满足条件：
①当n=0，1时，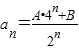
；
②当n≥2时（n∈N*，）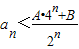
．如果存在，求出A，B的值，如果不存在，说明理由．
查看习题详情和答案>>
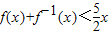，定义数列{an}，a=8，a1=10，an=f（an-1）（n∈N*）．（Ⅰ）求证：
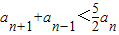（n∈N*）．（Ⅱ）设bn=an+1-2an（n∈N*），求证：bn＜（-6）•2-n（n∈N*）；
（Ⅲ）是否存在常数A，B同时满足条件：
①当n=0，1时，
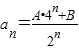；②当n≥2时（n∈N*，）
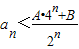．如果存在，求出A，B的值，如果不存在，说明理由．查看习题详情和答案>>
成立；②当n＝2、3、4、……，时，
成立．如果存在，求出A、B的值；如果不存在，说明理由．