摘要：解:①若两个角是对顶角.则这两个角相等． ②若四边形是平行四边形.则其对角线交于一点且互相平分． ③若一个数是偶数.则这个数能被2整除． ④若二次方程ax2+bx+c=0的判别式△>0.则该方程有两个不等实根．
网址：http://m.1010jiajiao.com/timu3_id_4465045[举报]
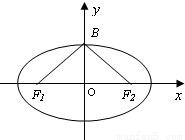
如图，已知椭圆
的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
（1）已知椭圆
和
判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
（2）写出与椭圆C1相似且半短轴长为b的椭圆Cb的方程，并列举相似椭圆之间的三种性质（不需证明）；
（3）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
查看习题详情和答案>>
的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．（1）已知椭圆
和判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；（2）写出与椭圆C1相似且半短轴长为b的椭圆Cb的方程，并列举相似椭圆之间的三种性质（不需证明）；
（3）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
查看习题详情和答案>>
如图，已知椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
（1）已知椭圆C1：
| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
（2）写出与椭圆C1相似且半短轴长为b的椭圆Cb的方程，并列举相似椭圆之间的三种性质（不需证明）；
（3）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
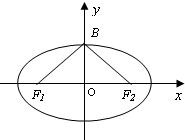如图，已知椭圆C：
+
=1（a＞b＞0）的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
+y2=1和C2：
+
=1，判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
+
=1（a＞b＞0）的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
+y2=1和C2：
+
=1，判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
+
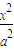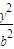=1（a＞b＞0）的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
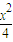+y2=1和C2：
+
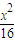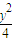=1，判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；