摘要:在平面直角坐标系中.到x轴的距离是到y轴距离的2倍的点P(x.y)的轨迹方程是A.x-2y=0 B.2x-y=0 C.|x|-2|y|=0 D.2|x|-|y|=0
网址:http://m.1010jiajiao.com/timu3_id_4464859[举报]
在平面直角坐标系中,已知焦距为4的椭圆C:
+
=1 (a>b>0)的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为
.
(1)求椭圆C的方程;
(2)设Q(t,m)是直线x=9上的点,直线QA、QB与椭圆C分别交于点M、N,求证:直线MN
必过x轴上的一定点,并求出此定点的坐标;
(3)实际上,第(2)小题的结论可以推广到任意的椭圆、双曲线以及抛物线,请你对抛物线y2=2px(p>0)写出一个更一般的结论,并加以证明. 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 3 |
(1)求椭圆C的方程;
(2)设Q(t,m)是直线x=9上的点,直线QA、QB与椭圆C分别交于点M、N,求证:直线MN
必过x轴上的一定点,并求出此定点的坐标;
(3)实际上,第(2)小题的结论可以推广到任意的椭圆、双曲线以及抛物线,请你对抛物线y2=2px(p>0)写出一个更一般的结论,并加以证明. 查看习题详情和答案>>
在平面直角坐标系中,点P到两点(-
,0),(
,0)的距离之和等于4,设点P的轨迹为C.
(1)写出C的轨迹方程;
(2)已知x轴上的一定点A(1,0),Q为轨迹C上的动点,求AQ中点M的轨迹方程.
查看习题详情和答案>>
| 3 |
| 3 |
(1)写出C的轨迹方程;
(2)已知x轴上的一定点A(1,0),Q为轨迹C上的动点,求AQ中点M的轨迹方程.
在平面直角坐标系中,O为坐标原点.已知曲线C上任意一点P(x,y)(其中x≥0)到定点F(1,0)的距离比它到y轴的距离大1.
(1)求曲线C的轨迹方程;
(2)若过点F(1,0)的直线l与曲线C相交于不同的A,B两点,求
•
的值;
(3)若曲线C上不同的两点M、N满足
•
=0,求|
|的取值范围.
查看习题详情和答案>>
(1)求曲线C的轨迹方程;
(2)若过点F(1,0)的直线l与曲线C相交于不同的A,B两点,求
| OA |
| OB |
(3)若曲线C上不同的两点M、N满足
| OM |
| MN |
| ON |
 中,已知曲线
中,已知曲线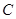 上任意一点到点
上任意一点到点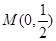 的距离与到直线
的距离与到直线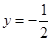 的距离相等.
的距离相等.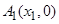 ,
,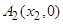 是
是 轴上的两点
轴上的两点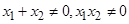 ,过点
,过点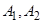 分别作
分别作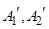 ,直线
,直线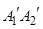 与x轴交于点
与x轴交于点 ,这样就称
,这样就称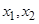 确定了
确定了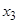 .同样,可由
.同样,可由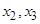 确定了
确定了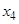 .现已知
.现已知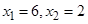 ,求
,求 中,已知双曲线
中,已知双曲线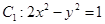 .
.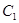 的左顶点引
的左顶点引 相切,求证:
相切,求证: . 若M、N分别是
. 若M、N分别是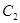 上的动点,且OM⊥ON,
上的动点,且OM⊥ON,