摘要:设点P,若点P在x轴上.则a= ;若点P在第四象限.则a 的取值范围是 .
网址:http://m.1010jiajiao.com/timu3_id_446425[举报]
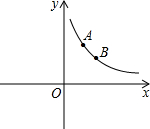 已知:如图,点A(m,3)与点B(n,2)关于直线y=x对称,且都在反比例函数y=
已知:如图,点A(m,3)与点B(n,2)关于直线y=x对称,且都在反比例函数y=| k | x |
(1)求反比例函数的解析式;
(2)若点P在x轴上,且S△AOP=6,直接写出点P的坐标.
如图1,直线L:y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线G:y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)该抛物线G的解析式为
(2)将直线L沿y轴向下平移
个单位长度,能使它与抛物线G只有一个公共点;
(3)若点E在抛物线G的对称轴上,点F在该抛物线上,且以点A、B、E、F为顶点的四边形为平行四边形,求点E与点F坐标并直接写出平行四边形的周长.
(4)连接AC,得△ABC.若点Q在x轴上,且以点P、B、Q为顶点的三角形与△ABC相似,求点Q的坐标.
查看习题详情和答案>>
(1)该抛物线G的解析式为
y=x2-4x+3
y=x2-4x+3
;(2)将直线L沿y轴向下平移
| 9 |
| 4 |
| 9 |
| 4 |
(3)若点E在抛物线G的对称轴上,点F在该抛物线上,且以点A、B、E、F为顶点的四边形为平行四边形,求点E与点F坐标并直接写出平行四边形的周长.
(4)连接AC,得△ABC.若点Q在x轴上,且以点P、B、Q为顶点的三角形与△ABC相似,求点Q的坐标.

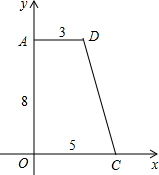 如图,在平面直角坐标系内放置一个直角梯形AOCD,已知AD=3,AO=8,OC=5.
如图,在平面直角坐标系内放置一个直角梯形AOCD,已知AD=3,AO=8,OC=5.(1)若点P在y轴上且S△PAD=S△poc,求点P的坐标;
(2)若点P在梯形内且S△PAD=S△POC,S△PAO=S△PCD,求点P的坐标.
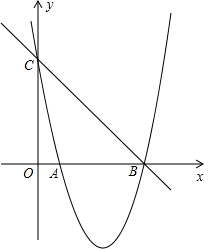 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0).另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0).另一个交点为A,且与y轴交于点C(0,5).