摘要：14．设函数.则方程的解为:
网址：http://m.1010jiajiao.com/timu3_id_4464056[举报]
设函数y=f （x）是定义域为R的奇函数，且满足f （x-2）=-f （x）对一切x∈R恒成立，当-1≤x≤1时，f （x）=x3，则下列四个命题：
①f（x）是以4为周期的周期函数．
②f（x）在[1，3]上的解析式为f （x）=（2-x）3．
③f（x）在(
，f(
))处的切线方程为3x+4y-5=0．
④f（x）的图象的对称轴中，有x=±1，其中正确的命题是（ ）
①f（x）是以4为周期的周期函数．
②f（x）在[1，3]上的解析式为f （x）=（2-x）3．
③f（x）在(
| 3 |
| 2 |
| 3 |
| 2 |
④f（x）的图象的对称轴中，有x=±1，其中正确的命题是（ ）
| A、①②③ | B、②③④ |
| C、①③④ | D、①②③④ |
设函数f（x）=ax+
（a，b∈Z），曲线y=f（x）在点（2，f（2））处的切线方程为y=3．
（Ⅰ）求f（x）的解析式，并判断函数y=f（x）的图象是否为中心对称图形？若是，请求其对称中心；否则说明理由．
（II）证明：曲线y=f（x）上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值，并求出此定值．
（III） 将函数y=f（x）的图象向左平移一个单位后与抛物线y=ax2（a为非0常数）的图象有几个交点？（说明理由）
查看习题详情和答案>>
| 1 | x+b |
（Ⅰ）求f（x）的解析式，并判断函数y=f（x）的图象是否为中心对称图形？若是，请求其对称中心；否则说明理由．
（II）证明：曲线y=f（x）上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值，并求出此定值．
（III） 将函数y=f（x）的图象向左平移一个单位后与抛物线y=ax2（a为非0常数）的图象有几个交点？（说明理由）
设函数y=f（x）是定义域为R 的奇函数，且满足f(x-2)=-f(x)对一切x∈R恒成立，当
-1≤x≤1时，f(x)=x3。则下列四个命题：①f(x)是以4为周期的周期函数；②f(x)在[1，3]上的解析式为f(x)=(2-x)3；③f(x)在
处的切线方程为3x+4y-5=0；④f(x)的图像的对称轴中有x=±1.其中正确的命题是 （ ）
A．① ② ③ B．② ③ ④ C．① ③ ④ D．① ② ③ ④
查看习题详情和答案>>
（a，b∈Z），曲线y=f（x）在点（2，f（2））处的切线方程为y=3．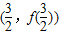
处的切线方程为3x+4y-5=0．