摘要:22.[解](1)对于非零常数T.f(x+T)=x+T, Tf(x)=Tx. 因为对任意x∈R.x+T= Tx不能恒成立.所以f(x)= (2)因为函数f(x)=ax(a>0且a≠1)的图象与函数y=x的图象有公共点. 所以方程组:有解.消去y得ax=x, 显然x=0不是方程ax=x的解.所以存在非零常数T.使aT=T. 于是对于f(x)=ax有 故f(x)=ax∈M. (3)当k=0时.f(x)=0.显然f(x)=0∈M. 当k≠0时.因为f(x)=sinkx∈M.所以存在非零常数T.对任意x∈R.有 f(x+T)=T f(x)成立.即sin(kx+kT)=Tsinkx . 因为k≠0.且x∈R.所以kx∈R.kx+kT∈R. 于是sinkx ∈[-1.1].sin(kx+kT) ∈[-1.1]. 故要使sin(kx+kT)=Tsinkx .成立. 只有T=.当T=1时.sin(kx+k)=sinkx 成立.则k=2mπ, m∈Z . 当T=-1时.sin(kx-k)=-sinkx 成立. 即sin(kx-k+π)= sinkx 成立. 则-k+π=2mπ, m∈Z .即k=-2(m-1) π, m∈Z . 综合得.实数k的取值范围是{k|k= mπ, m∈Z}
网址:http://m.1010jiajiao.com/timu3_id_4463741[举报]
已知集合M是满足下列性质的函数f(x)的全体:存在非零常数T,对任意x∈R,有f(x+T)=Tf(x)成立
(1)函数f(x)=x是否属于集合M?说明理由;
(2)设f(x)∈M,且T=2,已知当1<x<2时,f(x)=x+lnx,求当-3<x<-2时,f(x)的解析式.
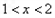 时, f(x)=x+lnx, 求当
时, f(x)=x+lnx, 求当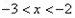 时, f(x)的解析式.
时, f(x)的解析式.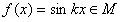 ,求实数k的取值范围.
,求实数k的取值范围.