摘要:26.某学习小组在探索“各内角相等的圆内接多边形是否为正多边形 时.进行如下讨论: 甲同学:这种多边形不一定是正多边形.如圆内接矩形, 乙同学:我发现边数是6时.它也不一定是正多边形. 如右图.ΔABC是正三角形.AD=BE=CF.可以证明六边形ADBECF的各内角相等.但它未必是正六边形, 丙同学:我能证明.边数是5时.它是正多边形.我想.边数是7时.它可能也是正多边形. -- (1)请你说明乙同学构造的六边形各内角相等. (2)请你证明.各内角都相等的圆内接七边形ABCDEFG是正七边形. (3)根据以上探索过程提出你的猜想. G O C A 27.如图.AB是⊙O的直径.BC是⊙O的弦.⊙O的割线PDE垂直AB于点F.交BC于点G.连结PC.∠BAC=∠BCP.求解下列问题: F P D E (1)求证:CP是⊙O的切线. B (2)当∠ABC=30°.BG=.CG=时.求以PD.PE的长为两根的一元二次方程. 的条件不变.当点C在劣弧AD上运动时.应再具备什么条件可使结论BG2=BF·BO成立?试写出你的猜想.并说明理由. 附加题:探究数学“黑洞 “黑洞 原指非常奇怪的天体.它体积小.密度大.吸引力强.任何物体到了它那里都别想再“爬 出来.无独有偶.数学中也有类似的“黑洞 .满足条件的所有数.通过一种运算.都能被它“吸 进去.无一能逃脱它的魔掌.譬如:任意找一个3的倍数的数.先把这个数的每个数位上的数字都立方.再相加.得到一个新数.然后把这个新数的每个数位上的数字再立方.再相加.得到一个新数.然后把这个新数的每个数位上的数字再立方.求和.--.重复运算下去.就能得到一个固定的数T= .我们称它为数字“黑洞 . 你愿意把得到上述结论的探究方法与他人交流吗?若愿意.请在横线上写出这个数并在下方简单写出你的探究过程.(结论正确且所写的过程敏捷合理可另加分.)
网址:http://m.1010jiajiao.com/timu3_id_446348[举报]
某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是6时,它也不一定是正多边形,如图1,△ABC是正三角形,
=
=
,证明六边形ADBECF的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是5时,它是正多边形,我想…,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图2)是正七边形;(不必写已知,求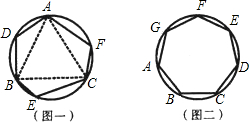 证)
证)
(3)根据以上探索过程,提出你的猜想.(不必证明) 查看习题详情和答案>>
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是6时,它也不一定是正多边形,如图1,△ABC是正三角形,
 |
| AD |
 |
| BE |
 |
| CF |
丙同学:我能证明,边数是5时,它是正多边形,我想…,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图2)是正七边形;(不必写已知,求
 证)
证)(3)根据以上探索过程,提出你的猜想.(不必证明) 查看习题详情和答案>>
(2013•婺城区一模)某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,有如下探讨:

甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:我知道,边数为3时,它是正三角形;我想,边数为5时,它可能也是正五边形…
丙同学:我发现边数为6时,它也不一定是正六边形.如图2,△ABC是正三角形,弧AD、弧BE、弧CF均相等,这样构造的六边形ADBECF不是正六边形.
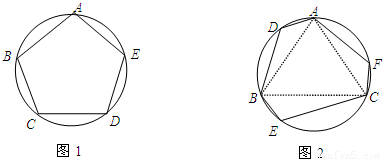
(1)如图1,若圆内接五边形ABCDE的各内角均相等,则∠ABC=
(2)如图2,请证明丙同学构造的六边形各内角相等.
(3)根据以上探索过程,就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,提出你的猜想(不需证明).
查看习题详情和答案>>

甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:我知道,边数为3时,它是正三角形;我想,边数为5时,它可能也是正五边形…
丙同学:我发现边数为6时,它也不一定是正六边形.如图2,△ABC是正三角形,弧AD、弧BE、弧CF均相等,这样构造的六边形ADBECF不是正六边形.
(1)如图1,若圆内接五边形ABCDE的各内角均相等,则∠ABC=
108°
108°
,请简要说明圆内接五边形ABCDE为正五边形的理由.(2)如图2,请证明丙同学构造的六边形各内角相等.
(3)根据以上探索过程,就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,提出你的猜想(不需证明).
某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,有如下探讨:

甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:我知道,边数为3时,它是正三角形;我想,边数为5时,它可能也是正五边形…
丙同学:我发现边数为6时,它也不一定是正六边形.如图2,△ABC是正三角形,弧AD、弧BE、弧CF均相等,这样构造的六边形ADBECF不是正六边形.
(1)如图1,若圆内接五边形ABCDE的各内角均相等,则∠ABC=______,请简要说明圆内接五边形ABCDE为正五边形的理由.
(2)如图2,请证明丙同学构造的六边形各内角相等.
(3)根据以上探索过程,就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,提出你的猜想(不需证明).
查看习题详情和答案>>
某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是6时,它也不一定是正多边形,如图1,△ABC是正三角形,
=
=
,证明六边形ADBECF的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是5时,它是正多边形,我想…,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图2)是正七边形;(不必写已知,求 证)
证)
(3)根据以上探索过程,提出你的猜想.(不必证明)
查看习题详情和答案>>
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是6时,它也不一定是正多边形,如图1,△ABC是正三角形,
 |
| AD |
 |
| BE |
 |
| CF |
丙同学:我能证明,边数是5时,它是正多边形,我想…,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图2)是正七边形;(不必写已知,求
 证)
证)(3)根据以上探索过程,提出你的猜想.(不必证明)
某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,有如下探讨:
甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:我知道,边数为3时,它是正三角形;我想,边数为5时,它可能也是正五边形…
丙同学:我发现边数为6时,它也不一定是正六边形.如图2,△ABC是正三角形,弧AD、弧BE、弧CF均相等,这样构造的六边形ADBECF不是正六边形.
(1)如图1,若圆内接五边形ABCDE的各内角均相等,则∠ABC=______,请简要说明圆内接五边形ABCDE为正五边形的理由.
(2)如图2,请证明丙同学构造的六边形各内角相等.
(3)根据以上探索过程,就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,提出你的猜想(不需证明).
查看习题详情和答案>>

甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:我知道,边数为3时,它是正三角形;我想,边数为5时,它可能也是正五边形…
丙同学:我发现边数为6时,它也不一定是正六边形.如图2,△ABC是正三角形,弧AD、弧BE、弧CF均相等,这样构造的六边形ADBECF不是正六边形.
(1)如图1,若圆内接五边形ABCDE的各内角均相等,则∠ABC=______,请简要说明圆内接五边形ABCDE为正五边形的理由.
(2)如图2,请证明丙同学构造的六边形各内角相等.
(3)根据以上探索过程,就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,提出你的猜想(不需证明).
查看习题详情和答案>>