摘要：已知:抛物线与x轴交于A.B两点.与y轴交于点C． (1)求A.B.C三点的坐标, (2)如果直线:y＝x+b过点A.判断它与双曲线有没有交点.如果有交点.求出交点坐标,如果没有交点.请说明理由, 中的直线l和双曲线分别交于点E.F.直线FD∥y轴.交l于点D．当t的取值变化时.设△CDE的面积为S.写出S与t的函数关系式.并求出自变量t的取值范围．(抛物线的对称轴是与y轴平行的直线.类似的.直线y＝t是与x轴平行的直线．)
网址：http://m.1010jiajiao.com/timu3_id_446278[举报]
（本小题满分14分）
已知：如图，抛物线
与y轴交于点C（0，
）， 与x轴交于点A、 B，点A的坐标为（2，0）．
（1）求该抛物线的解析式；
（2）点P是线段AB上的动点，过点P作PD∥BC，交AC于点D，连接CP．当△CPD的面积最大时，求点P的坐标；
（3）若平行于x轴的动直线
与该抛物线交于点Q，与直线BC交于点F，点M 的坐标为（
，0）．问：是否存在这样的直线，使得△OMF是等腰三角形？若存 在，请求出点Q的坐标；若不存在，请说明理由．
查看习题详情和答案>>
（本小题满分14分）
已知：如图，抛物线与y轴交于点C（0，
）， 与x轴交于点A、 B，点A的坐标为（2，0）．
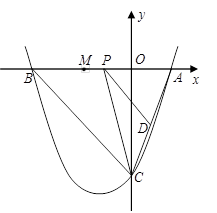
（1）求该抛物线的解析式；
（2）点P是线段AB上的动点，过点P作PD∥BC，交AC于点D，连接CP．当△CPD的面积最大时，求点P的坐标；
（3）若平行于x轴的动直线与该抛物线交于点Q，与直线BC交于点F，点M 的坐标为（
，0）．问：是否存在这样的直线
，使得△OMF是等腰三角形？若存 在，请求出点Q的坐标；若不存在，请说明理由．
查看习题详情和答案>>
（本小题满分14分）
如图，已知抛物线y＝ax2＋bx＋c与x轴交于A（－1，0），B（3，0）两点，与y轴交于点C（0，3）。设抛物线的顶点为D，求解下列问题：
1.（1）求抛物线的解析式和D点的坐标；
2.（2）过点D作DF∥
轴，交直线BC于点F，求线段DF的长，并求△BCD的面积；
3.（3）能否在抛物线上找到一点Q，使△BDQ为直角三角形？若能找到，试写出Q点的坐标；若不能，请说明理由。
查看习题详情和答案>>
轴，交直线BC于点F，求线段DF的长，并求△BCD的面积；
与y轴交于点C（0，
）， 与x轴交于点A、 B，点A的坐标为（2，0）．
与该抛物线交于点Q，与直线BC交于点F，点M 的坐标为（
，0）．问：是否存在这样的直线