摘要:21.如图.已知A.B.C是长轴长为4的椭圆上的三点.点A是长 轴的一个端点.BC过椭圆中心O.且满足AC⊥BC.|BC|=2|AC|. ⑴ 建立适当的坐标系.求椭圆的方程, ⑵ 如果P.Q是该椭圆上异于A.B的两点.使∠PCQ的平分线垂直于OA. 求证:PQ∥AB.
网址:http://m.1010jiajiao.com/timu3_id_4462442[举报]
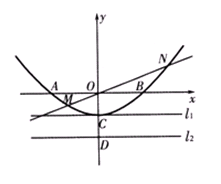
(本小题满分14分) 如图,已知抛物线与坐标轴分别交于A 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;
.(1)求抛物线对应的二次函数的解析式;
(2)求证以ON为直径的圆与直线 相切;
相切;
(3)求线段MN的长(用 表示),并证明M、N两
表示),并证明M、N两
点到直线 的距离之和等于线段MN的长.
的距离之和等于线段MN的长.

查看习题详情和答案>>
(本小题满分14分) 如图,已知抛物线与坐标轴分别交于A 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D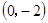 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线
.(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线 相切;(3)求线段MN的长(用
相切;(3)求线段MN的长(用 表示),并证明M、N两点到直线
表示),并证明M、N两点到直线 的距离之和等于线段MN的长.
的距离之和等于线段MN的长.

查看习题详情和答案>>
(本小题满分14分) 如图,已知抛物线与坐标轴分别交于A 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线
.(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线 相切;(3)求线段MN的长(用
相切;(3)求线段MN的长(用 表示),并证明M、N两点到直线
表示),并证明M、N两点到直线 的距离之和等于线段MN的长.
的距离之和等于线段MN的长.
 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;
.(1)求抛物线对应的二次函数的解析式; 表示),并证明M、N两
表示),并证明M、N两
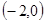 、B
、B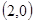 、C
、C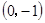 三点,过坐标原点O的直线
三点,过坐标原点O的直线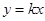 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D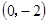 作平行于
作平行于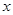 轴的直线
轴的直线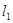 、
、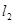 .(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线
.(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线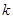 表示),并证明M、N两点到直线
表示),并证明M、N两点到直线