摘要:10.已知.那么 . 又若.那么 .
网址:http://m.1010jiajiao.com/timu3_id_4462357[举报]
如果以数列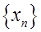 的任意连续三项作边长,都能构成一个三角形,那么称这样的数列
的任意连续三项作边长,都能构成一个三角形,那么称这样的数列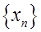 为“三角形”数列;又对于“三角形”数列
为“三角形”数列;又对于“三角形”数列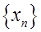 ,如果函数y=f(x)使得由
,如果函数y=f(x)使得由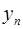 =f(
=f(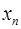 )(
)(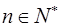 )确定的数列
)确定的数列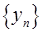 仍成为一个“三角形”数列,就称y=f(x) 是数列
仍成为一个“三角形”数列,就称y=f(x) 是数列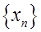 的“保三角形”函数。
的“保三角形”函数。
(Ⅰ)、已知数列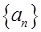 是首项为2012,公比为
是首项为2012,公比为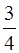 的等比数列,求证:
的等比数列,求证: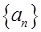 是“三角形”数列;
是“三角形”数列;
(Ⅱ)、已知数列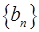 是首项为2,公差为1的等差数列,若函数f(x)=
是首项为2,公差为1的等差数列,若函数f(x)= 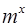 (m>0且m≠1)是
(m>0且m≠1)是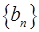 的“保三角形”函数. 求m的取值范围.
的“保三角形”函数. 求m的取值范围.
查看习题详情和答案>>
如果以数列 的任意连续三项作边长,都能构成一个三角形,那么称这样的数列
的任意连续三项作边长,都能构成一个三角形,那么称这样的数列 为“三角形”数列;又对于“三角形”数列
为“三角形”数列;又对于“三角形”数列 ,如果函数y=f(x)使得由
,如果函数y=f(x)使得由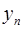 =f(
=f( )(
)( )确定的数列
)确定的数列 仍成为一个“三角形”数列,就称y="f(x)" 是数列
仍成为一个“三角形”数列,就称y="f(x)" 是数列 的“保三角形”函数。
的“保三角形”函数。
(Ⅰ)、已知数列 是首项为2012,公比为
是首项为2012,公比为 的等比数列,求证:
的等比数列,求证: 是“三角形”数列;
是“三角形”数列;
(Ⅱ)、已知数列 是首项为2,公差为1的等差数列,若函数f(x)=
是首项为2,公差为1的等差数列,若函数f(x)= (m>0且m≠1)是
(m>0且m≠1)是 的“保三角形”函数. 求m的取值范围.
的“保三角形”函数. 求m的取值范围.
 的任意连续三项作边长,都能构成一个三角形,那么称这样的数列
的任意连续三项作边长,都能构成一个三角形,那么称这样的数列 为“三角形”数列;又对于“三角形”数列
为“三角形”数列;又对于“三角形”数列 ,如果函数y=f(x)使得由
,如果函数y=f(x)使得由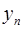 =f(
=f( )(
)( )确定的数列
)确定的数列 仍成为一个“三角形”数列,就称y="f(x)" 是数列
仍成为一个“三角形”数列,就称y="f(x)" 是数列 的“保三角形”函数。
的“保三角形”函数。(Ⅰ)、已知数列
 是首项为2012,公比为
是首项为2012,公比为 的等比数列,求证:
的等比数列,求证: 是“三角形”数列;
是“三角形”数列;(Ⅱ)、已知数列
 是首项为2,公差为1的等差数列,若函数f(x)=
是首项为2,公差为1的等差数列,若函数f(x)= (m>0且m≠1)是
(m>0且m≠1)是 的“保三角形”函数. 求m的取值范围.
的“保三角形”函数. 求m的取值范围.已知 ,函数
,函数
(1)当 时,求函数
时,求函数 在点(1,
在点(1, )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在 上至少存在一个实数x0,使
上至少存在一个实数x0,使 >g(xo)成立,求正实数
>g(xo)成立,求正实数 的取值范围。
的取值范围。
【解析】本试题中导数在研究函数中的运用。(1)中 ,那么当
,那么当 时,
时, 又
又  所以函数
所以函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 ;(2)中令
;(2)中令 有
有 

对a分类讨论 ,和
,和 得到极值。(3)中,设
得到极值。(3)中,设 ,
, ,依题意,只需
,依题意,只需 那么可以解得。
那么可以解得。
解:(Ⅰ)∵ ∴
∴ 
∴ 当 时,
时, 又
又 
∴ 函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 --------4分
--------4分
(Ⅱ)令 有
有 

①
当 即
即 时
时
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故 的极大值是
的极大值是 ,极小值是
,极小值是
②
当 即
即 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为 ,无极小值。
,无极小值。
综上所述  时,极大值为
时,极大值为 ,无极小值
,无极小值
 时 极大值是
时 极大值是 ,极小值是
,极小值是 ----------8分
----------8分
(Ⅲ)设 ,
,
对 求导,得
求导,得
∵ ,
,

∴  在区间
在区间 上为增函数,则
上为增函数,则
依题意,只需 ,即
,即
解得  或
或 (舍去)
(舍去)
则正实数 的取值范围是(
的取值范围是(
 ,
, )
)
查看习题详情和答案>>

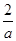 )
)

