摘要：(1)常数T满足 和,则T的一个值是( )． (A) (B) (C) (D) (2)在等差数列 中. ,则 的值为( )． 20 (D) (3)设点P对应复数是,以原点为极点.实轴的正半轴为极轴.建立极坐 标系.则点P的极坐标为( )． (A) (B) (C) (D) (4)设A.B是两个非空集合.若规定:,则 等于( )． (A) (B) (C) (D) (5)函数的图象与直线的交点个数为( )． 0或1 (6)设函数(其中),则是为 奇函数的( )． 必要不充分条件 既不充分也不必要条件 (7)如图.在斜三棱柱中.∠BAC＝90°..过作 底面ABC.垂足为.则( )． (A)在直线AC上 (B)在直线AB上 (C)在直线BC上 (D)在△ABC内 (8)电讯资费调整后.市话费标准为:通话时间不超过3分钟收费0.2元,超 过3分钟.以后每增加1分钟收费0.1元.不足1分钟以1分钟收费.则通话收S(元)与通话时间t的函数图象可表示为( )． (9)以椭圆的右焦点为圆心.且与双曲线的渐近线相 切的圆的方程为( )． (A) (B) (C) (D) (10)已知的展开式中所有项系数之和为729.则这个展开式中含项 的系数是( )． 160 (D)180 (11)AB是过圆锥曲线焦点F的弦.l是与点F对应的准线.则以弦AB为直 径的圆与直线l的位置关系( )． 相离 (D)由离心率e决定 (12)定义在R上的函数的反函数为.则是( )． 偶函数 满足题设的函数不存在 第II卷
网址：http://m.1010jiajiao.com/timu3_id_4461582[举报]
（2008•奉贤区模拟）我们规定：对于任意实数A，若存在数列{an}和实数x（x≠0），使得A=a1+a2x+a3x2+…+anxn-1，则称数A可以表示成x进制形式，简记为：A=
．如：A=
，则表示A是一个2进制形式的数，且A=-1+3×2+（-2）×22+1×23=5．
（1）已知m=（1-2x）（1+3x2）（其中x≠0），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，ak+1=
，k∈N*，bn=
（n∈N*），是否存在实常数p和q，对于任意的n∈N*，bn=p•8n+q总成立？若存在，求出p和q；若不存在，说明理由．
（3）若常数t满足t≠0且t＞-1，dn=
，求
．
查看习题详情和答案>>
. |
| x\～(a1)(a2)(a3)…(an-1)(an) |
. |
| 2\～(-1)(3)(-2)(1) |
（1）已知m=（1-2x）（1+3x2）（其中x≠0），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，ak+1=
| 1 |
| 1-ak |
. |
| 2\～(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
（3）若常数t满足t≠0且t＞-1，dn=
. | ||||||||||
t\～(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
（2008•奉贤区一模）我们规定：对于任意实数A，若存在数列{an}和实数x（x≠0），使得A=a1+a2x+a3x2+…+anxn-1，则称数A可以表示成x进制形式，简记为：A=
．如：A=
，则表示A是一个2进制形式的数，且A=-1+3×2+（-2）×22+1×23=5．
（1）已知m=（1-2x）（1+3x2）（其中x≠0）），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，ak+1=
，k∈N*，bn=
（n∈N*）．求证：bn=
•8n-
．
（3）若常数t满足t≠0且t＞-1，dn=
，求
．
查看习题详情和答案>>
. |
| x\～(a1)(a2)(a3)…(an-1)(an) |
. |
| 2\～(-1)(3)(-2)(1) |
（1）已知m=（1-2x）（1+3x2）（其中x≠0）），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，ak+1=
| 1 |
| 1-ak |
. |
| 2\～(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
| 2 |
| 7 |
| 2 |
| 7 |
（3）若常数t满足t≠0且t＞-1，dn=
. | ||||||||||
t\～(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
我们规定：对于任意实数A，若存在数列{an}和实数x（x≠0），使得A=a1+a2x+a3x2+…+anxn-1，则称数A可以表示成x进制形式，简记为：
．如：
，则表示A是一个2进制形式的数，且A=-1+3×2+（-2）×22+1×23=5．
（1）已知m=（1-2x）（1+3x2）（其中x≠0）），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，
，
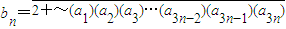（n∈N*）．求证：
．
（3）若常数t满足t≠0且t＞-1，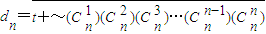
，求
．
查看习题详情和答案>>
．如：，则表示A是一个2进制形式的数，且A=-1+3×2+（-2）×22+1×23=5．（1）已知m=（1-2x）（1+3x2）（其中x≠0）），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，
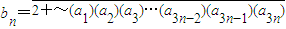，（n∈N*）．求证：．（3）若常数t满足t≠0且t＞-1，
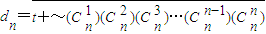，求．查看习题详情和答案>>
我们规定：对于任意实数A，若存在数列{an}和实数x（x≠0），使得A=a1+a2x+a3x2+…+anxn-1，则称数A可以表示成x进制形式，简记为：A=
．如：A=
，则表示A是一个2进制形式的数，且A=-1+3×2+（-2）×22+1×23=5．
（1）已知m=（1-2x）（1+3x2）（其中x≠0），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，ak+1=
，k∈N*，bn=
（n∈N*），是否存在实常数p和q，对于任意的n∈N*，bn=p•8n+q总成立？若存在，求出p和q；若不存在，说明理由．
（3）若常数t满足t≠0且t＞-1，dn=
，求
．
查看习题详情和答案>>
| . |
| x\～(a1)(a2)(a3)…(an-1)(an) |
| . |
| 2\～(-1)(3)(-2)(1) |
（1）已知m=（1-2x）（1+3x2）（其中x≠0），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，ak+1=
| 1 |
| 1-ak |
| . |
| 2\～(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
（3）若常数t满足t≠0且t＞-1，dn=
| . | ||||||||||
t\～(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
我们规定：对于任意实数A，若存在数列{an}和实数x（x≠0），使得A=a1+a2x+a3x2+…+anxn-1，则称数A可以表示成x进制形式，简记为：A=
．如：A=
，则表示A是一个2进制形式的数，且A=-1+3×2+（-2）×22+1×23=5．
（1）已知m=（1-2x）（1+3x2）（其中x≠0）），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，ak+1=
，k∈N*，bn=
（n∈N*）．求证：bn=
•8n-
．
（3）若常数t满足t≠0且t＞-1，dn=
，求
．
查看习题详情和答案>>
| . |
| x\～(a1)(a2)(a3)…(an-1)(an) |
| . |
| 2\～(-1)(3)(-2)(1) |
（1）已知m=（1-2x）（1+3x2）（其中x≠0）），试将m表示成x进制的简记形式．
（2）若数列{an}满足a1=2，ak+1=
| 1 |
| 1-ak |
| . |
| 2\～(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
| 2 |
| 7 |
| 2 |
| 7 |
（3）若常数t满足t≠0且t＞-1，dn=
| . | ||||||||||
t\～(
|
| lim |
| n→∞ |
| dn |
| dn+1 |