摘要:(1)双曲线的两个焦点坐标分别是() (A).(B). (2)下列四个函数中.在区间 (A)(B)y=sinx (C)(D)y=arccosx (3)如果复数(其中i为虚数单位.b为实数)的实部和虚部互为相反数.那么b等于() (A)(B) (C)(D)2 (4)α.β是两个不重合的平面.在下列条件中.可判定平面α与β平行的是() (A)m.n是α内两条直线.且m∥β.n∥β (B)α.β都垂直于平面γ (C)α内不共线三点到β的距离都相等 (D)m.n是两条异面直线...且m∥β.n∥α (5)函数的最大值是() (A)(B) 2 (6)在等比数列中...则的值是() (A)(B) (C)(D) (7)某人制定了一项旅游计划.从7个旅游城市中选择5个进行游览.如果A.B为必选城市.并且在游览过程中必须按先A后B的次序经过A.B两城市.则有不同的游览线路() 240种 600种 (8)设偶函数在上单调递减.则f的大小关系是() f 不能确定 (9)P是双曲线右支上一点..分别是左.右焦点.且焦距为2c.则的内切圆圆心的横坐标为() b a+b-c 的定义域为D.如果对于任意的.存在唯一的.使成立.则称函数y=f(x)在D上的均值为C.给出下列四个函数: ①,②y=4sinx, ③y=lgx,④ 则满足在其定义域上均值为2的所有函数是() ③④ ①③
网址:http://m.1010jiajiao.com/timu3_id_4460859[举报]
过双曲线C:
-
=1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 ______.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
设F1、F2分别为椭圆C:
+
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线
-
=1写出具有类似特性的性质,并加以证明.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
(1)若椭圆C上的点A(1,
| 3 |
| 2 |
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线
| x2 |
| a2 |
| y2 |
| b2 |
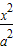 -
-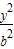 =1(a>b>0)的两个焦点,A和B是以O(O为坐标原点)为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则双曲线的离心率为( )
=1(a>b>0)的两个焦点,A和B是以O(O为坐标原点)为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则双曲线的离心率为( )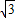
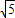
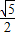
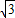 +1
+1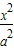 -
-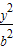 =1(a>b>0)的两个焦点,A和B是以O(O为坐标原点)为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则双曲线的离心率为( )
=1(a>b>0)的两个焦点,A和B是以O(O为坐标原点)为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则双曲线的离心率为( )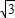
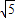
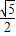
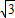 +1
+1