摘要： 甲.乙两名射手在一次射击中的得分是两个随机变量,分别记为和,它们的分布列分别为 0 1 2 P 0.1 a 0.4 0 1 2 P 0.2 0.2 b (1) 求a , b 的值 (2) 计算和的期望与方差,并以此分析甲.乙两射手的技术情况.
网址：http://m.1010jiajiao.com/timu3_id_4460855[举报]
(本题满分12分) 在某次射击比赛中共有5名选手，出场时甲、乙、丙三人不能相邻。求（1）共有多少种不同的出场顺序？
（2）若甲、乙、丙三人每次射击命中目标的概率都为0.6,求三人各射击一次至少有一
人命中目标的概率。
（3）若甲、乙、丙三人每次射击命中目标的概率分别为0.7,0.6,0.5，求三人各射击一
次至少有两人命中目标的概率。
查看习题详情和答案>>
(本题满分12分)在某次射击比赛中共有5名选手，出场时甲、乙、丙三人不能相邻。求（1）共有多少种不同的出场顺序？
（2）若甲、乙、丙三人每次射击命中目标的概率都为0.6,求三人各射击一次至少有一
人命中目标的概率。
（3）若甲、乙、丙三人每次射击命中目标的概率分别为0.7,0.6,0.5，求三人各射击一
次至少有两人命中目标的概率。
（2）若甲、乙、丙三人每次射击命中目标的概率都为0.6,求三人各射击一次至少有一
人命中目标的概率。
（3）若甲、乙、丙三人每次射击命中目标的概率分别为0.7,0.6,0.5，求三人各射击一
次至少有两人命中目标的概率。
（本小题满分12分）
甲、乙两名射手各进行一次射击，射中环数
的分布列分别为：
 | 8 | 9 | 10 |
| P | 0．3 | 0．5 | a |
 | 8 | 9 | 10 |
| P | 0．2 | 0．3 | b |
）确定a、b的值，并求两人各进行一次射击，都射中10环的概率；（II）两各射手各射击一次为一轮射击，如果在某一轮射击中两人都射中10环，则射击结束，否则继续射击，但最多不超过4轮，求结束时射击轮次数
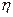的分布列及期望，并求结束时射击轮次超过2次的概率。
查看习题详情和答案>>
的分布列分别为：
）确定a、b的值，并求两人各进行一次射击，都射中10环的概率；
的分布列及期望，并求结束时射击轮次超过2次的概率。
，乙的命中率为
，在射击比武活动中每人射击两发子弹则完成一次检测，在一次检测中，若两人命中次数相等且都不少于一发，则称该射击小组为“先进和谐组”.
，求该小组在一次检测中荣获“先进和谐组”的概率；
， 
，求