摘要:20. 在直角坐标系中.O为坐标原点.设直线经过点.且与轴交于点 (I)求直线的方程, (II)如果一个椭圆经过点,且以点为它的一个焦点,求椭圆的标准方程; .情形下.设直线与椭圆的另一个交点为.且.当 最小时.求对应的值.
网址:http://m.1010jiajiao.com/timu3_id_4457925[举报]
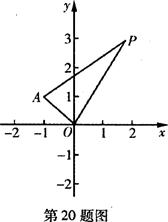
(本小题满分14分)在平面直角坐标系xOy中,已知点A(-1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.
( I)求点P的轨迹C的方程;
(Ⅱ)若Q是轨迹C上异于点P的一个点,且 ,直线OP与QA交于点M,问:是否存在点P使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
,直线OP与QA交于点M,问:是否存在点P使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
查看习题详情和答案>>
(本小题满分14分)在周长为定值的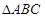 中,已知
中,已知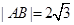 ,动点
,动点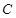 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点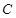 运动时,
运动时,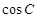 有最小值
有最小值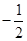 .
.
(1) 以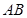 所在直线为
所在直线为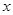 轴,线段
轴,线段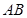 的中垂线为
的中垂线为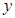 轴建立直角坐标系,求曲线
轴建立直角坐标系,求曲线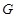 的方程;
的方程;
(2) 过点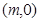 作圆
作圆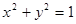 的切线
的切线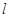 交曲线
交曲线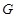 于
于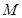 ,
,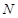 两点.将线段MN的长|MN|表示为
两点.将线段MN的长|MN|表示为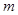 的函数,并求|MN|的最大值.
的函数,并求|MN|的最大值.
查看习题详情和答案>>
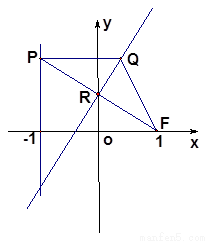
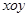 中,设点
中,设点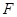 (1,0),直线
(1,0),直线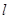 :
: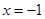 ,点
,点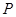 在直线
在直线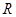 是线段
是线段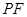 与
与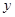 轴的交点,
轴的交点,  .
.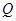 的轨迹方程;
的轨迹方程;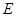 ,过点
,过点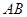 、
、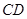 ,设
,设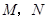 .求证:直线
.求证:直线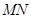 必过定点
必过定点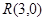 .
.
 中,已知
中,已知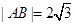 ,动点
,动点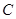 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点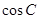 有最小值
有最小值 .
.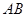 所在直线为
所在直线为 轴,线段
轴,线段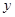 轴建立直角坐标系,求曲线G的方程.
轴建立直角坐标系,求曲线G的方程.