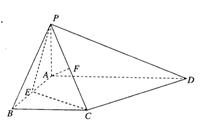
摘要:17. 如图.在四棱锥P-ABCD中.平面PAD⊥平面ABCD, ..E是BD的中点. (Ⅰ)求证:EC//平面APD, (Ⅱ)求BP与平面ABCD所成角的正切值, (Ⅲ) 求二面角P-AB-D的大小. 解法一:(Ⅰ)如图.取PA中点F.连结EF.FD. ∵E是BP的中点. ∵EF//AB且. 又∵ ∴EFDC∴四边形EFDC是平行四边形.故得EC//FD ----2分 又∵EC平面PAD.FD平面PAD ∴EC//平面ADE ----4分 (Ⅱ)取AD中点H.连结PH.因为PA=PD.所以PH⊥AD ∵平面PAD⊥平面ABCD于AD ∴PH⊥面ABCD ∴HB是PB在平面ABCD内的射影 ∴∠PBH是PB与平面ABCD所成角 ----6分 ∵四边形ABCD中. ∴四边形ABCD是直角梯形 设AB=2a.则. 在中,易得, . 又∵. ∴是等腰直角三角形. ∴ ∴在中. ----10分 (Ⅲ)在平面ABCD内过点H作AB的垂线交AB于G点.连结PG.则HG是PG在平面ABCD上的射影.故PG⊥AB.所以∠PGH是二面角P-AB-D的平面角.由AB=2a ----11分 .又∴ 在中. 13分 ∴二面角P-AB-D的大小为 ----14分 解法二:(Ⅰ)同解法一 4分 (Ⅱ)设AB=2a.同解法一中的(Ⅱ)可得 如图.以D点为原点.DA所在直线为x轴.DB所在直线为y轴.过D点且垂直于平面ABCD的直线为z轴建立空间直角坐标系. ----5分 则..则.平面ABCD的一个法向量为m=. ----7分 所以. 可得PB与平面ABCD所成角的正弦值为 所以 PB与平面ABCD所成角的正切值为 ----10分 (Ⅲ)易知.则.设平面PAB的一个法向量为.则 .令.可得--12分 得. 所以二面角P-AB-D的大小为----14分
网址:http://m.1010jiajiao.com/timu3_id_4457008[举报]
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,![]() 为AB中点,F为PC中点.
为AB中点,F为PC中点.
(I)求证:PE⊥BC;
(II)求二面角C—PE—A的余弦值;
(III)若四棱锥P—ABCD的体积为4,求AF的长.

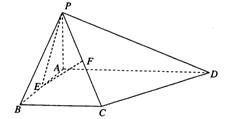
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,AD>BC,E,F分别为棱AB,PC的中点.
(I)求证:PE⊥BC;
(II)求证:EF//平面PAD.
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,AD>BC,E,F分别为棱AB,PC的中点.
(I)求证:PE⊥BC;
(II)求证:EF//平面PAD.
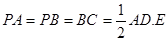 为AB中点,F为PC中点.
为AB中点,F为PC中点.