摘要：9．函数对都有.若.. 则数列的前n项和的极限是( ). A． B． C． D．
网址：http://m.1010jiajiao.com/timu3_id_4456731[举报]
函数f（x）是定义在R上恒不为0的函数，对任意x，y∈R都有f（x）·f（y）=f（x+y），若a1=
，
an=f（n）（n∈N*），则数列{an}的前n项和Sn的取值范围是
，an=f（n）（n∈N*），则数列{an}的前n项和Sn的取值范围是
[ ]
A.[
，1]
B.[
，2]
C.[
，1）
D.[
，2）
查看习题详情和答案>>
，1]B.[
，2]C.[
，1）D.[
，2）已知数列{an}中，点P（an，an+1）在函数f（x）=x+2图象上，数列{bn}前n项和为Sn，且a1=2，bn，Sn成等差数列．
（1）求数列{an}，{bn}的通项公式；
（2）设Cn=
，{Cn}前n项和为Tn．问是否存在最小的正整数m，使对任意 n∈N*都有Tn＜m．若存在，求出m的值，否则，说明理由．
查看习题详情和答案>>
（1）求数列{an}，{bn}的通项公式；
（2）设Cn=
| an | bn |
已知数列{an}中，点P（an，an+1）在函数f（x）=x+2图象上，数列{bn}前n项和为Sn，且a1=2，bn，Sn成等差数列．
（1）求数列{an}，{bn}的通项公式；
（2）
．问是否存在最小的正整数m，使对任意 n∈N*都有Tn＜m．若存在，求出m的值，否则，说明理由．
查看习题详情和答案>>
（1）求数列{an}，{bn}的通项公式；
（2）
．问是否存在最小的正整数m，使对任意 n∈N*都有Tn＜m．若存在，求出m的值，否则，说明理由．查看习题详情和答案>>
已知函数f（x）是定义在（0，+∞）上的单调函数，且对任意的正数x，y都有f=f（x）+f（y），若数列{an}的前n项和为sn，且满足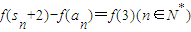
，则an为 （ ）
A．2n-1
B．n
C．2n-1
D．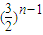
查看习题详情和答案>>
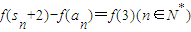，则an为 （ ）A．2n-1
B．n
C．2n-1
D．
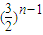
查看习题详情和答案>>
观察数列：
①1，－1，1，－1…；
②正整数依次被4除所得余数构成的数列1，2，3，0，1，2，3，0，…；
③
(1)对以上这些数列所共有的周期特征，请你类比周期函数的定义，为这类数列下一个周期数列的定义：对于数列{an}，如果________，对于一切正整数n都满足________成立，则称数列{an}是以T为周期的周期数列；
(2)若数列{an}满足an+2＝an+1－an，n∈N+，Sn为{an}的前n项和，且S2＝2008，S3＝2010，证明{an}为周期数列，并求S2008；
(3)若数列{an}的首项
，且an+1＝2an(1－an)，n∈N*，判断数列{an}是否为周期数列，并证明你的结论．