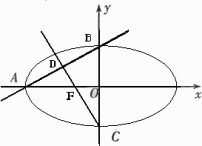
摘要：如图.椭圆的离心率e=左焦点为F.A.B.C为其三个顶点.直线CF与AB交于D.则tan∠BDC的值等于( ) A． B． C． D． 第 Ⅱ 卷
网址：http://m.1010jiajiao.com/timu3_id_4456665[举报]
(a＞b＞o)的离心率e＝
左焦点为F，A，B，C为其三个顶点，直线CF与AB交于D，则tan∠BDC的值等于
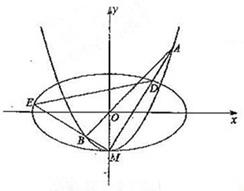如图，椭圆C1：| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
（Ⅰ）求C1，C2的方程；
（Ⅱ）设C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A、B，直线MA，MB分别与C1相交于D，E．
（i）证明：MD⊥ME；
（ii）记△MAB，△MDE的面积分别是S1，S2．问：是否存在直线l，使得
| S1 |
| S2 |
| 17 |
| 32 |
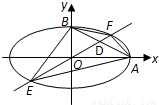
如图，椭圆的中心在坐标原点O，左右焦点分别为F1，F2，右顶点为A，上顶点为B，离心率
，三角形△BF1F2的周长为16．直线y=kx（k＞0）与AB相交于点D，与椭圆相交于E，F两点．
（1）求该椭圆的标准方程．
（2）求四边形AEBF面积的最大值．
查看习题详情和答案>>
，三角形△BF1F2的周长为16．直线y=kx（k＞0）与AB相交于点D，与椭圆相交于E，F两点．（1）求该椭圆的标准方程．
（2）求四边形AEBF面积的最大值．
查看习题详情和答案>>
=1（a＞b＞0）的离心率为
，x轴被曲线C2：y=x2-b截得的线段长等于C1的长半轴长．
=
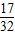？请说明理由．
=1（a＞b＞0）的离心率为
，x轴被曲线C2：y=x2-b截得的线段长等于C1的长半轴长．
=
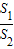？请说明理由．