摘要：20．已知定义在R上的函数(a.b.c.)的图象关于原点对称.且当时.取得极小值. (Ⅰ)求的单调递增区间, (Ⅱ)解关于x的不等式．
网址：http://m.1010jiajiao.com/timu3_id_4456652[举报]
已知定义在R上的函数
(a，b，c，d为实常数)的图象关于原点对称，且当x＝1时f(x)取得极值
.
（Ⅰ）求函数f(x)的解析式；
（Ⅱ）证明：对任意
∈[－1，1]，不等式
成立；
（Ⅲ）若函数
在区间(1，∞)内无零点，求实数m的取值范围.
已知定义在R上的函数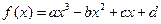
(a，b，c，d为实常数)的图象关于原点对称，且当x＝1时f(x)取得极值
.
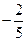（Ⅰ）求函数f(x)的解析式；
（Ⅱ）证明：对任意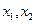
∈[－1，1]，不等式
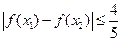成立；
（Ⅲ）若函数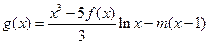
在区间(1，∞)内无零点，求实数m的取值范围.
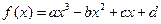(a，b，c，d为实常数)的图象关于原点对称，且当x＝1时f(x)取得极值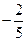.（Ⅰ）求函数f(x)的解析式；
（Ⅱ）证明：对任意
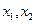∈[－1，1]，不等式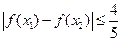成立；（Ⅲ）若函数
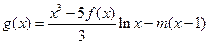在区间(1，∞)内无零点，求实数m的取值范围.27、已知定义在R上的函数y=f（x）满足下列三个条件：①对任意的x∈R都有f（x）=f（x+4）；②对于任意的0≤x1＜x2≤2，都有f（x1）＜f（x2），③y=f（x+2）的图象关于y轴对称，则下列结论中，正确的是（ ）
查看习题详情和答案>>
已知定义在R上的函数f（x）满足f（x）+f（-x）=0，f（x+1）=-f（x），且当0＜x＜
时，f（x）=lgx；设a=f(
)，b=f(
)，c=f(
)，则（ ）
| 1 |
| 2 |
| 6 |
| 5 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜a＜b |
| D、c＜b＜a |
